ACインダクタ

インダクタを含む回路を考え、コイル線を含む回路の抵抗が無視できるほど小さいと仮定します。この場合、コイルを直流電源に接続すると短絡が発生し、周知のとおり、回路内の電流が非常に大きくなります。

コイルが AC 電源に接続されている場合は状況が異なります。この場合、短絡は発生しません。これは示しています。インダクタは、それを通過する交流電流に対してどれだけ抵抗しますか。

この抵抗の本質は何でしょうか、またそれはどのように条件づけられているのでしょうか?

この質問に答えるには、次のことを思い出してください。自己誘導現象… コイル内の電流が変化すると、コイル内に自己誘導の EMF が発生し、電流の変化が妨げられます。自己誘導のEMFの値は次の値に正比例します。コイルのインダクタンス値そしてその中の電流の変化率。しかしそれ以来交流電流連続的に変化するコイル内に継続的に現れる自己誘導の電磁波が交流に対する抵抗を生み出します。

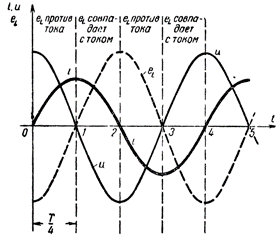
で行われているプロセスを理解するには、交流回路インダクタについては、グラフを参照してください。図1は、回路内のマーク、コイル内の電圧、コイル内で発生する自己誘導起電力をそれぞれ特徴付ける曲線を示しています。図で作られた構造が正しいことを確認してみましょう。

インダクタを使用した交流回路

t = 0 の瞬間、つまり電流を観測した最初の瞬間から電流は急激に増加し始めますが、最大値に近づくにつれて電流の増加率は減少します。電流が最大値に達した瞬間、その変化率が瞬間的にゼロとなり、電流の変化が止まる。その後、電流は最初はゆっくりと始まり、その後急速に減少し、期間の第 2 四半期後にはゼロに下がりました。期間のこの四半期中の電流の変化率は、弾丸から増加し、電流がゼロになったときに最高値に達します。

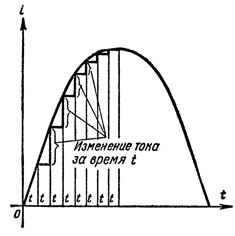
電流の大きさに応じた、時間の経過に伴う電流の変化の性質

図 2. 電流の大きさに応じた、時間の経過に伴う電流の変化の性質

図 2 の構成から、電流曲線が時間軸を通過するとき、電流曲線がピークに達する同じ期間よりも短い期間 T で電流が増加することがわかります。

したがって、回路内の電流の方向に関係なく、電流の変化率は電流が増加すると減少し、電流が減少すると増加します。

コイルの自己インダクタンスの起電力は、電流の変化率が最大になるときに最大になり、変化が止まるとゼロに減少することは明らかです。実際、グラフ上の自己誘導 eL の EMF 曲線は、期間の最初の四半期で、最大値からゼロまで低下します (図 1 を参照)。

期間の次の 4 分の 1 では、電流は最大値からゼロまで減少しますが、その変化率は徐々に増加し、電流がゼロになった瞬間に最大になります。したがって、周期のこの 4 分の 1 の間、コイル内に再び現れる自己誘導の EMF は徐々に増加し、電流がゼロになるまで最大になります。

ただし、期間の第 1 四半期の電流増加が第 2 四半期には減少したため、自己誘導起電力の方向は逆方向に変化しました。

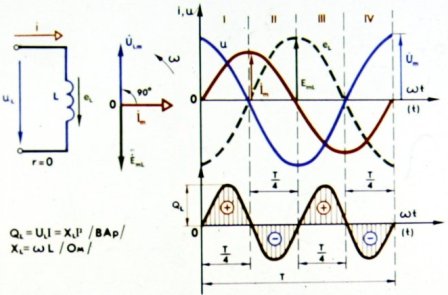
インダクタンスを伴う回路

自己誘導の起電力曲線の構築をさらに続けると、コイル内の電流とコイル内の自己誘導の起電力の変化期間中に、その変化の全期間が完了すると確信します。その方向性は決まっているレンツの法則: 電流が増加すると、自己誘導起電力は電流に逆らうようになります (期間の第 1 四半期と第 3 四半期)。電流が減少すると、逆に電流の方向と一致します (期間の第 2 四半期と第 4 四半期)。

そのため、交流自体による自己誘導起電力が増加を防ぎ、逆に下降時には維持されます。

ACインダクタ

次に、コイル電圧のグラフを見てみましょう (図 1 を参照)。このグラフでは、コイル端子電圧の正弦波が自己インダクタンス起電力の正弦波と等しく、逆になっていることが示されています。したがって、コイルの端子の電圧はどの瞬間でも等しく、コイル内で発生する自己誘導の EMF と逆になります。この電圧はオルタネーターによって生成され、EMF 自己誘導回路の動作を抑制します。

したがって、交流回路に接続されたインダクタには電流が流れると抵抗が発生します。しかし、この抵抗は最終的にコイルのインダクタンスを誘導するため、誘導抵抗と呼ばれます。

誘導抵抗は XL で示され、抵抗としてオーム単位で測定されます。

回路の誘導抵抗が大きいほど、電流源周波数回路の電源と回路のインダクタンスが大きくなります。したがって、回路の誘導抵抗は、電流の周波数と回路のインダクタンスに直接比例します。は公式 XL = ωL によって決定されます。ここで、ω — 積 2πe… によって決定される円周周波数 — n における回路インダクタンス。

オームの法則誘導抵抗を含む AC 回路の場合、音は次のようになります。電流量は電圧に正比例し、NSi の誘導抵抗に反比例します。 I = U / XL、ここで、I と U は実効電流値と実効電圧値、xL は回路の誘導抵抗です。

コイルに流れる電流の変化のグラフを考えてみましょう。自己誘導のEMFとその端子の電圧、それらのvValueの変化が時間的に一致しないという事実に注意を払いました。言い換えれば、検討中の回路では、電流、電圧、および自己誘導起電力正弦波が相互に時間的にシフトしていることが判明しました。 AC テクノロジーでは、この現象は一般に位相シフトと呼ばれます。

2 つの変数量が同じ法則 (この場合は正弦波) に従って同じ周期で変化し、順方向と逆方向の両方で同時に最大値に達し、同時にゼロに減少する場合、そのような変数量は同じ位相を持つ、または、彼らが言うように、位相が一致します。

例として、図 3 に位相整合した電流と電圧の曲線を示します。能動抵抗のみからなる交流回路では、このような位相整合が常に観察されます。

図に示すように、回路に誘導抵抗、電流位相、電圧位相が含まれる場合、 1 は一致しません。つまり、これらの変数間に位相シフトがあります。この場合の電流曲線は、電圧曲線よりも周期の 4 分の 1 遅れているように見えます。

したがって、AC回路にインダクタが含まれる場合、回路内で電流と電圧の間に位相シフトが発生し、電流は電圧よりも周期の4分の1遅れます。これは、最大電流が4分の1発生することを意味します。最大電圧に達した後の期間。

自己誘導の起電力はコイルの電圧と逆位相で、電流より周期の 4 分の 1 遅れます。この場合、電流、電圧、起電力の変化の周期は、コイルの電圧と逆位相になります。自己誘導は変化せず、回路に電力を供給する発電機の電圧の変化周期と同じままです。これらの値の変化の正弦波の性質も維持されます。

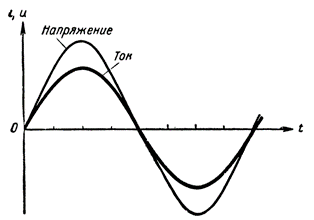
アクティブ抵抗回路における電流と電圧の位相整合

図 3. アクティブ抵抗回路における電流と電圧の位相整合

ここで、能動抵抗を伴うオルタネーター負荷と誘導抵抗を伴う負荷の違いを理解しましょう。

AC 回路にアクティブ抵抗が 1 つだけ含まれている場合、電流源のエネルギーはアクティブ抵抗に吸収されます。ワイヤーを加熱する.

ACインダクタ

回路に能動抵抗が含まれておらず (通常はゼロであると考えられます)、コイルの誘導抵抗のみで構成されている場合、電流源のエネルギーはワイヤの加熱には費やされず、自己誘導の EMF を生成することだけに費やされます。つまり、磁場のエネルギーになります...ただし、交流は大きさと方向の両方が常に変化しているため、磁場コイルは電流の変化に合わせて連続的に変化します。期間の最初の 4 分の 1 の間、電流が増加すると、回路は電流源からエネルギーを受け取り、それをコイルの磁場に蓄積します。しかし、最大値に達した電流が減少し始めるとすぐに、自己誘導起電力によってコイルの磁場に蓄えられたエネルギーを犠牲にして電流が維持されます。

したがって、電流源は周期の第 1 四半期に回路にエネルギーの一部を与え、第 2 四半期にコイルからエネルギーを受け取り、一種の電流源として機能します。言い換えれば、誘導抵抗のみを含む交流回路はエネルギーを消費しません。この場合、電源と回路の間にエネルギーの変動が存在します。逆に、アクティブ抵抗は、電流源から転送されるすべてのエネルギーを吸収します。

インダクタは、オーミック抵抗とは異なり、AC 電源に対して不活性であると言われます。リアクティブ... したがって、コイルの誘導抵抗はリアクタンスとも呼ばれます。

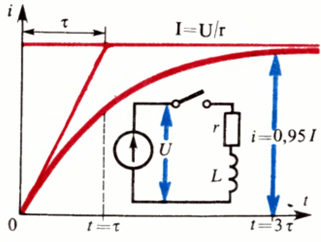
インダクタンスを含む回路を閉じるときの電流上昇曲線 — 電気回路の過渡現象.