アクティブおよびリアクティブ抵抗、三角抵抗
 活性と反応性
活性と反応性
DC回路のパスと消費者によって提供される抵抗は、オーム抵抗と呼ばれます。
AC 回路にワイヤが含まれている場合、その抵抗は DC 回路よりもわずかに高くなることがわかります。これは表皮効果と呼ばれる現象によるものです(表面効果).
その本質は次のとおりです。交流電流がワイヤを流れると、ワイヤの内部に交流磁場が存在し、ワイヤを横切ります。この磁場の磁力線は導体内に EMF を引き起こしますが、導体の断面の異なる点では EMF は同じではありません。断面の中心に向かうほど大きくなり、外周に向かうほど小さくなります。
これは、中心近くにある点が多数の力線と交差するという事実によるものです。この EMF の作用により、交流は導体の断面全体に均一に分布するのではなく、その表面近くに分布します。
これは、導体の有効断面積が減少し、したがって交流に対する抵抗が増加することに相当します。たとえば、長さ 1 km、直径 4 mm の銅線の抵抗は、DC — 1.86 オーム、AC 800 Hz — 1.87 オーム、AC 10,000 Hz — 2.90 オームです。
導体を通過する交流に対して導体が与える抵抗は、アクティブ抵抗と呼ばれます。
消費者にインダクタンスとキャパシタンスが含まれていない場合 (白熱電球、加熱装置)、それもアクティブな AC 抵抗になります。
能動抵抗 — 電気エネルギーが他の形態 (主に熱) に不可逆的に変換されることによる、電流に対する電気回路 (またはその領域) の抵抗を特徴付ける物理量。オームで表されます。
アクティブ抵抗は次のものに依存します 交流周波数増加に伴い増加します。
ただし、多くの消費者は、交流電流が流れると誘導性および容量性の特性を持ちます。これらの消費者には、変圧器、チョーク、 電磁石, コンデンサ、さまざまな種類のワイヤー、その他多数。
それらを通過するとき 交流電流 消費者には誘導性および容量性の特性が存在するため、能動性だけでなく反応性も考慮する必要があります。
各コイルに流れる直流電流を遮断して閉じると、電流が変化すると同時にコイル内の磁束も変化し、その結果自己誘導起電力が発生することが知られています。初期化。
同じことが交流回路に含まれるコイルでも観察されますが、唯一の違いは、トルクの大きさと内外の両方が連続的に変化することです。したがって、コイルを貫く磁束の大きさは連続的に変化し、磁束を誘導します。 自己誘導起電力.
しかし、自己誘導起電力の方向は常に電流の変化に逆らう方向になります。したがって、コイル内の電流が増加すると、自己誘導EMFは電流の増加を遅くする傾向があり、逆に、電流が減少すると、消失電流を維持する傾向があります。
したがって、交流回路を構成するコイル(導体)に発生する自己誘導起電力は、常に電流に逆らって作用し、電流の変化を遅くすることになります。言い換えれば、自己誘導のEMFは、コイルの能動抵抗とともに、コイルを通過する交流に対抗する追加の抵抗と考えることができます。
起電力によって自己誘導によって交流に与えられる抵抗は、誘導抵抗と呼ばれます。
誘導抵抗は、ユーザー(回路)のインダクタンスが大きくなり、交流の周波数が高くなるほど大きくなります。この抵抗は式 xl = ωL で表されます。ここで、xl はオーム単位の誘導抵抗です。 L — ヘンリー単位のインダクタンス (gn)。 ω - 角周波数、f - 電流周波数)。
誘導抵抗に加えて、ワイヤやコイル内の静電容量の存在と、場合によっては AC 回路にコンデンサが含まれることにより、静電容量も存在します。消費者(回路)の静電容量 C と電流の角周波数が増加するにつれて、容量抵抗は減少します。
容量性抵抗は xc = 1 / ωC に等しくなります。ここで、xc - 容量性抵抗 (オーム)、ω - 角周波数、C - 消費者容量 (ファラッド)。
詳細については、こちらをご覧ください。 電気工学におけるリアクタンス
三角抵抗
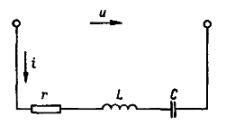
能動素子の抵抗が r、インダクタンスが L、容量が C である回路を考えます。
米。 1. 抵抗、インダクタ、コンデンサを含む AC 回路。
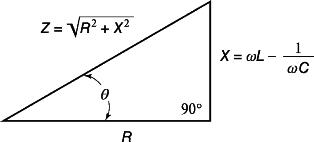
このような回路のインピーダンスは、z = √r2+ (хl — xc)2) = √r2 + х2) となります。
グラフ的には、この式はいわゆる抵抗三角形の形で表すことができます。
イチジク。 2. 三角抵抗
抵抗三角形の斜辺は、回路の合計抵抗、脚、つまりアクティブ抵抗とリアクティブ抵抗を表します。
たとえば、回路の一方の抵抗 (アクティブまたはリアクティブ) が他方の抵抗の 10 倍以上小さい場合、小さい方は無視でき、直接計算で簡単に確認できます。