電圧共振

交流回路が直列に接続されている場合 インダクタ と コンデンサ、その後、それらは独自の方法で、回路に電力を供給する発電機と、電流と電圧の間の位相接続に影響を与えます。

インダクタは位相シフトを引き起こし、電流が電圧より周期の 4 分の 1 遅れるのに対し、コンデンサは逆に、回路内の電圧を電流より周期の 4 分の 1 遅らせます。したがって、回路内の電流と電圧間の位相シフトに対する誘導抵抗の効果は、容量性抵抗の効果とは逆になります。

これは、回路内の電流と電圧の間の合計位相シフトが誘導性抵抗値と容量性抵抗値の比に依存するという事実につながります。

回路の容量性抵抗の値が誘導性抵抗の値よりも大きい場合、回路は本質的に容量性である、つまり、電圧は電流より位相が遅れています。逆に、回路の誘導抵抗が容量抵抗よりも大きい場合は、電圧が電流よりも進み、したがって回路は誘導性になります。

検討している回路の合計リアクタンス Xtot は、コイル XL の誘導抵抗とコンデンサ XC の容量抵抗を加算することによって決まります。

しかし、回路内のこれらの抵抗の作用は逆であるため、そのうちの 1 つ、つまり Xc にはマイナス記号が割り当てられ、合計リアクタンスは次の式で求められます。

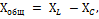
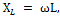
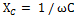
この回路に適用します オームの法則、 我々が得る：

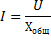
この式は次のように変形できます。

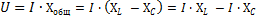
結果として得られる方程式では、AzxL — 回路の誘導抵抗を克服する回路の合計電圧の成分の実効値、AzNSC — 回路の合計電圧の成分の実効値、これは回路の誘導抵抗を克服します。容量性抵抗を克服します。

したがって、コイルとコンデンサの直列接続で構成される回路の総電圧は、2つの項で構成されていると考えることができ、その値はコイルの誘導性抵抗と容量性抵抗の値に依存します。回路。

私たちは、このような回路には能動抵抗がないと信じていました。ただし、回路のアクティブ抵抗が無視できるほど小さくない場合、回路の合計抵抗は次の式で求められます。

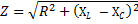
ここで、R は回路の合計アクティブ抵抗、XL -NSC - 合計リアクタンスです。オームの法則の公式に移ると、次のように書く権利があります。

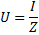
交流電圧共振

直列に接続された誘導性抵抗と容量性抵抗は、AC 回路に個別に含まれている場合よりも、AC 回路内の電流と電圧の間の位相シフトを小さくします。

つまり、回路内で性質の異なる 2 つの反応が同時に作用することにより、位相ずれの補償（相互破壊）が発生します。

全額補償、つまり。このような回路における電流と電圧間の位相シフトが完全に除去されるのは、誘導性抵抗が回路の容量性抵抗と等しい場合、つまり XL = XC の場合、または同様に ωL = 1 / ωC の場合です。

この場合、回路は純粋にアクティブな抵抗として動作します。つまり、コイルもコンデンサもないかのように動作します。この抵抗の値は、コイルと接続ワイヤのアクティブ抵抗の合計によって決まります。これで 実効電流 回路内では最大となり、オームの法則の公式 I = U / R によって決定されます。ここで、Z は R に置き換えられます。

同時に、コイル UL = AzxL とコンデンサ Uc = AzNSCC に作用する電圧は等しく、可能な限り大きくなります。回路のアクティブ抵抗が低いと、これらの電圧は回路端子の合計電圧 U を何倍も超える可能性があります。この興味深い現象は、電気工学では電圧共振と呼ばれます。

図では。図１は、回路内の共振電圧における電圧、電流、電力の曲線を示している。

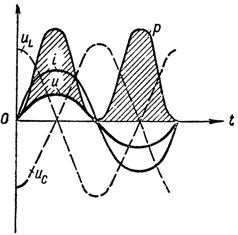
電圧共振時の電圧電流と電力のグラフ

抵抗 XL と C は電流の周波数に依存する変数であり、その周波数を少なくともわずかに変更する価値があることに留意する必要があります。たとえば、XL = ωL が増加し、XSC = = 1 のように周波数を増加します。 / ωC が減少するため、回路内の電圧共振が直ちに妨げられ、アクティブ抵抗とともに回路内にリアクタンスが発生します。回路のインダクタンスまたはキャパシタンスの値を変更した場合も同じことが起こります。

電圧共振では、電流源の電力は回路のアクティブ抵抗を克服するため、つまりワイヤを加熱するためだけに消費されます。

実際、単一の誘導コイルを備えた回路では、エネルギー変動が発生します。発電機から発電機へのエネルギーの周期的な伝達 磁場 コイル。コンデンサを備えた回路でも同じことが起こりますが、コンデンサの電界エネルギーが原因です。電圧共振 (ХL = XС) にあるコンデンサとインダクタを備えた回路では、回路に蓄えられたエネルギーは周期的にコイルからコンデンサへ、またはその逆に通過し、コイルの能動抵抗を克服するのに必要なエネルギーのみが消費されます。回路は電流源の一部を占めます。したがって、発電機の関与をほとんど受けずに、コンデンサとコイルの間でエネルギー交換が行われます。

値によって電圧共振を解消する必要があるのは、コイルの磁場のエネルギーがコンデンサの電場のエネルギーとどのように等しくないのか、そしてこれらの磁場間のエネルギー交換の過程で過剰なエネルギーが発生することだけです。回路内のソースから周期的に流れ出て、回路内のソースにフィードバックされます。

この現象は、時計仕掛けで起こる現象と非常によく似ています。時計の振り子は、動きを遅くする摩擦力がなければ、バネ (または時計歩行器の重り) の助けがなくても、継続的に振動することができます。

ばねは、適切な瞬間にそのエネルギーの一部を振り子に伝達することにより、振り子が摩擦力に打ち勝つのを助け、それによって振動の連続性を実現します。

同様に、電気回路内で共振が発生すると、電流源は回路のアクティブ抵抗を克服するためだけにエネルギーを消費し、回路内の振動プロセスを支援します。

したがって、発電機と直列接続されたインダクタとコンデンサで構成される交流回路は、特定の条件XL = XС下で発振システムになるという結論に達しました...この回路は発振回路と名付けられました。

方程式XL = XСから、電圧共振現象が発生する発電機の周波数の値を決定することができます。

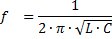
電圧共振が発生する回路の容量とインダクタンスを意味します。

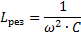
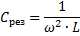
したがって、これら 3 つの量 (eres、L、C) のいずれかを変更することで、回路内で電圧共振を引き起こす、つまり回路を発振回路にすることができます。

電圧共振の有用な応用例: 受信機の入力回路は、電圧共振が発生するように可変コンデンサ (またはバリオメーター) によって調整されます。これにより、アンテナによって生成される回路電圧と比較して、通常の受信機動作に必要なコイル電圧が大幅に増加します。

電気工学における電圧共振現象の有用な利用に加えて、電圧共振が有害である場合もよくあります。発電機の故障により、別の部品や測定装置が損傷する可能性があります。