インダクタンスの計算方法

力学において質量を持つ物体が空間の加速に抵抗して慣性を示すのと同じように、インダクタンスは導体の電流の変化を妨げ、自己誘導起電力を示します。これは自己誘導の EMF であり、電流を維持しようとする電流の減少と、電流を減少させようとする電流の増加の両方に抵抗します。

実際には、回路内の電流が変化（増加または減少）する過程で、この電流によって生成される磁束も変化し、主にこの回路によって制限された領域に局在します。そして、磁束が増加または減少すると、同じ回路内で (レンツの法則に従って、磁束を引き起こす原因、つまり冒頭で述べた電流に対して) 自己誘導の EMF が誘導されます。ここでのインダクタンス L は、電流 I と総磁束 Φ の間の比例係数と呼ばれます。この電流は次のように生成されます。

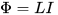
したがって、回路のインダクタンスが高いほど、結果として生じる磁場よりも強くなり、電流の変化が妨げられます（電流を生み出すのは磁場です）。したがって、インダクタンスが大きくなると電流が変化するのに時間がかかります。同じ印加電圧で。次の記述も当てはまります。インダクタンスが大きいほど、回路を通る磁束が変化したときに回路にかかる電圧が大きくなります。

特定の領域の磁束を一定の割合で変化させ、この領域をさまざまな回路でカバーすると、インダクタンスが大きいその回路でより多くの電圧が得られるとします（変圧器、ラムコルフコイルなどはこの原理で動作します）。

しかし、ループインダクタンスはどのように計算されるのでしょうか?電流と磁束の間の比例係数を見つけるにはどうすればよいですか?最初に覚えておくべきことは、インダクタンスはヘンリー (H) で変化するということです。インダクタンスが 1 ヘンリーの回路の端子では、回路内の電流が 1 秒あたり 1 アンペア変化すると、1 ボルトの電圧が発生します。

インダクタンスの大きさは、回路の幾何学的寸法 (長さ、幅、巻き数など) と媒体の磁気特性 (たとえば、内部にフェライト コアがある場合) の 2 つのパラメータによって決まります。コイルのインダクタンスは、内部にコアがない場合よりも大きくなります)。

生成されるインダクタンスを計算するには、コイル自体がどのような形状になるか、およびコイル内の媒体がどのような透磁率を持つかを知る必要があります (媒体の比透磁率は、真空の透磁率と磁気の透磁率の間の比例係数です)。特定の媒体の透過性。もちろん素材によっても異なります）…

最も一般的な形式のコイル (円筒形ソレノイド、トロイド、長いワイヤ) のインダクタンスを計算する式を見てみましょう。

インダクタンスの計算式は次のとおりです。 ソレノイド — コイルの長さが直径よりもはるかに長い場合:

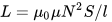
ご覧のとおり、巻き数 N、巻線の長さ l、コイルの断面積 S がわかると、コアなしまたはコアありのコイルのおおよそのインダクタンスがわかります。真空の透磁率は一定の値です。

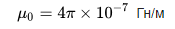
トロイダル コイルのインダクタンス。ここで、h はトロイドの高さ、r はトロイドの内径、R はトロイドの外径です。

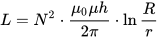
細いワイヤ (断面の半径が長さよりもはるかに小さい) のインダクタンス、l はワイヤの長さ、r は断面の半径です。Mu とインデックス i および e は次のとおりです。内部 (内部、導体材料) および外部 (外部、導体の外側の材料) 環境の相対透磁率:

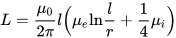
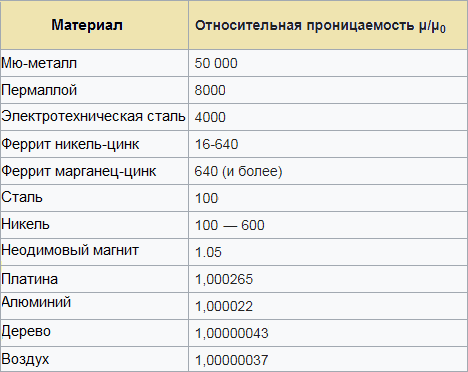
比誘電率の表は、特定の磁性材料をコアとして使用した回路 (ワイヤ、コイル) からどのようなインダクタンスが予想されるかを見積もるのに役立ちます。