AC回路のアクティブ抵抗とインダクタ

誘導抵抗のみを含む交流回路を考える（記事を参照） ≪交流回路におけるインダクタ≫)、この回路のアクティブ抵抗はゼロであると仮定しました。

実際、コイル自体のワイヤと接続ワイヤの両方には小さいながらもアクティブな抵抗があるため、回路は必然的に電流源のエネルギーを消費します。

したがって、外部回路の合計抵抗を決定するときは、その無効抵抗とアクティブ抵抗を追加する必要があります。しかし、性質の異なるこれら 2 つの抵抗を追加することは不可能です。

この場合、交流に対する回路のインピーダンスは幾何加算によって求められます。

直角三角形 (図 1 を参照) が作成され、その一方の辺が誘導抵抗の値、もう一方の辺が能動抵抗の値になります。必要な回路インピーダンスは、三角形の 3 番目の辺によって決まります。

図 1. 誘導抵抗と能動抵抗を含む回路のインピーダンスの決定

回路インピーダンスはラテン文字 Z で示され、オーム単位で測定されます。この構造から、合計抵抗は、個別に計算した誘導抵抗と能動抵抗よりも常に大きいことがわかります。

回路の総抵抗の代数式は次のとおりです。

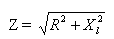
ここで、Z - 合計抵抗、R - アクティブ抵抗、XL - 回路の誘導抵抗。

したがって、アクティブ抵抗と誘導抵抗からなる回路の交流に対する合計抵抗は、この回路のアクティブ抵抗と誘導抵抗の二乗の和の平方根に等しくなります。

オームの法則 このような回路は式 I = U / Z で表されるため、Z は回路の合計抵抗です。

ここで、回路に、電流とインダクタンス間の位相シフトに加えて、比較的大きなアクティブ抵抗がある場合、電圧はどうなるかを解析してみましょう。実際には、そのような回路は、例えば、細いワイヤで巻かれた鉄心インダクタを含む回路（高周波チョーク）であり得る。

この場合、電流と電圧の間の位相シフトは（誘導抵抗のみの回路の場合のように）周期の 4 分の 1 ではなくなり、はるかに小さくなります。抵抗が大きいほど、位相シフトは少なくなります。

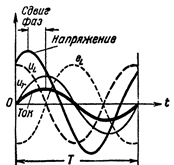
図2. RとLを含む回路の電流と電圧。

今では彼女自身が 自己誘導起電力 電流源電圧に対して半周期ではなくそれ未満オフセットしているため、電流源電圧と逆位相ではありません。さらに、電流源によってコイルの端子に生成される電圧は、自己誘導起電力と等しくありませんが、コイル線のアクティブ抵抗での電圧降下の分だけ自己誘導起電力より大きくなります。言い換えれば、コイル内の電圧はいずれにしても 2 つの成分で構成されます。

• tiL- 自己誘導による EMF の影響を平衡させる電圧の無効成分、

• tiR - 回路のアクティブ抵抗を克服する電圧のアクティブ成分。

大きなアクティブ抵抗をコイルに直列に接続すると、位相シフトが大幅に減少し、電流正弦波が電圧正弦波にほぼ追いつき、両者の位相差がほとんど目立たなくなります。項の振幅よりも大きくなります。

同様に、何らかの方法でジェネレータの周波数を下げれば、位相シフトを低減でき、完全にゼロにすることもできます。周波数が低下すると、自己誘導EMFが減少し、それによって生じる回路内の電流と電圧間の位相シフトが減少します。

インダクタを含むAC回路の電力

コイルを含む交流回路は電流源のエネルギーを消費せず、回路内では発電機と回路の間でエネルギー交換プロセスが行われます。

このようなスキームによって消費される電力がどうなるかを分析してみましょう。

AC回路で消費される電力は電流と電圧の積に等しいですが、電流と電圧は可変量であるため、電力も可変になります。この場合、特定の瞬間に対応する電流値と電圧値を乗算すると、各瞬間の電力値を求めることができます。

電力グラフを取得するには、さまざまな時点での電流と電圧を定義する直線セグメントの値を乗算する必要があります。このような構造を図に示します。 3、a.破線の波形 p は、誘導抵抗のみを含む AC 回路で電力がどのように変化するかを示しています。

この曲線の構築には次の代数乗算ルールが使用されました。正の値に負の値を乗算すると負の値が得られ、2 つの負の値または 2 つの正の値を乗算すると正の値が得られます。

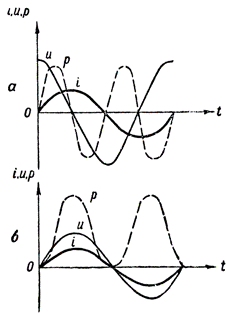
図 3. 電力グラフ: a — 誘導抵抗を含む回路内、b — アクティブ抵抗も含む

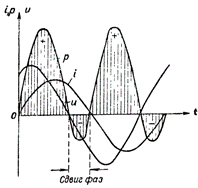
図 4. R と L を含む回路の電力プロット。

この場合の電力曲線は時間軸の上にあります。これは、発電機と回路の間でエネルギーの交換が存在しないことを意味し、したがって、発電機によって回路に供給された電力は回路によって完全に消費されます。

図では。図 4 は、誘導抵抗と能動抵抗の両方を含む回路の電力プロットを示しています。この場合、回路から電流源へのエネルギーの逆伝達も発生しますが、その程度は単一の誘導抵抗を備えた回路よりもはるかに小さいです。

上記の電力グラフを検討した結果、回路内の電流と電圧間の位相シフトのみが「負の」電力を生成すると結論付けられます。この場合、回路内の電流と電圧間の位相シフトが大きいほど、回路で消費される電力は少なくなり、逆に、位相シフトが小さいほど、回路で消費される電力は大きくなります。

こちらもお読みください: 電圧共振とは何ですか