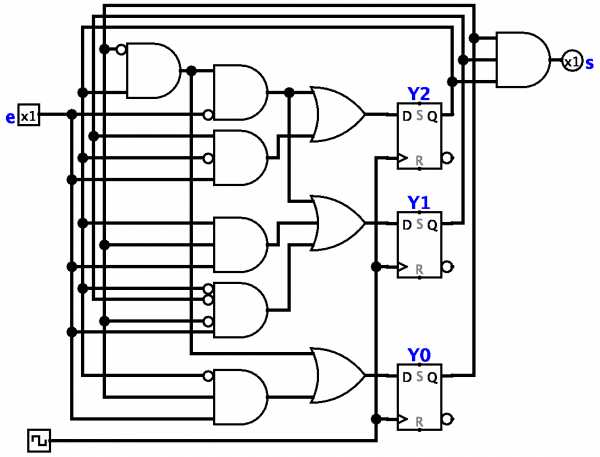
オートマトン、有限オートマトンの理論
さまざまな機械の構造、設計、動作原理は、主にその機能目的によって決まります。テクノロジー、輸送、コンピューティング、軍事、その他の機械を区別します。複雑な技術プロセスを実行するように設計された自動複合体全体が、さまざまな業界で広く導入されています。オートマトンは、さまざまな論理機能 (論理マシン) を実行するように設計および構築されます。
オートマトンの理論 — サイバネティクスセクション、デジタルコンピュータと制御機械の技術要件の影響下で発生しました。オートマトン理論で研究される離散オートマトンは、離散時間ステップで離散(デジタル)情報を処理する実際のシステム(技術的および生物学的)の抽象モデルです。
オートマトン理論は、オートマトンの機能 (動作) とその構造 (内部構造) についての直観的なアイデアを形式化する正確な数学的概念に基づいています。
この場合、情報変換は常に、入力アルファベットの文字で構成される入力シーケンスを、出力アルファベットの文字で構成される出力シーケンスに変換する操作として理解されます。
数理論理学、代数、確率論、組み合わせ論、グラフ理論の装置が広く使用されています。
オートマトンの理論(オートマトンの構造理論)の一部に問題が大きくなった リレー接点回路の理論より、1930年代後半に形になり始めました。包括的 論理代数の手法.

オートマトンの構造理論では、システム内で適切に接続された単純なコンポーネント (要素) から複雑なオートマトンがどのように作成されるかを説明するために設計された、さまざまなタイプのスキームが研究されます。
オートマトンの抽象理論と呼ばれるもう 1 つの方向は、オートマトンの内部構造の詳細を抽象化しながら、オートマトンの動作 (つまり、オートマタによって実行される情報の変換の性質) を研究するもので、1950 年代に生まれました。
オートマトンの抽象理論の枠組み内では、「オートマトン」と「機械」という概念の内容は、オートマトンによって実行される情報の変換の標準的な記述によって本質的に網羅されています。このような変換は決定論的である場合もありますが、本質的に確率論的である場合もあります。
最も研究されているのは決定論的機械 (オートマトン) で、これには有限オートマトンが含まれます。これはオートマトン理論の主な研究対象です。
有限状態マシンは、限られた量のメモリ (内部状態の数) を特徴とし、遷移関数を使用して定義されます。ある程度の合理的な理想化があれば、現代のすべての数学機械、さらには脳さえも、その機能の観点からは有限オートマトンとみなすことができます。
「シーケンシャル マシン」、「ミリー オートマトン」、「ムーア オートマトン」という用語は、文献内で (すべての著者によって一律にではありませんが) 「有限オートマトン」という用語の同義語として、または有限オートマトンの遷移関数における特定の機能を強調するために使用されています。オートマトン。
無制限のメモリを備えたオートマトンは、あらゆる効率的な情報変換を (潜在的に) 実行できるチューリング マシンです。 「チューリングマシン」の概念は「有限状態マシン」の概念よりも早く生まれ、主にアルゴリズム理論で研究されています。
抽象オートマトン理論は、半群理論などのよく知られた代数理論と密接に関連しています。応用的な観点からは、オートマトン内の情報の変換をメモリ サイズの観点から特徴付ける結果は興味深いものです。
これは、たとえば、オートマトンの実験 (E.F. ムーアなどによる研究) の問題の場合に当てはまります。オートマトンの遷移関数またはそのメモリ容量に関する何らかの情報が、オートマトンの結果から得られます。実験。
もう 1 つのタスクは、オートマトンのメモリ サイズと入力シーケンスの周期に関する利用可能な情報に基づいて、出力シーケンスの周期を計算することです。
非常に重要なのは、有限状態マシンのメモリを最小限に抑え、ランダムな環境での動作を研究する方法の開発です。
抽象オートマトン理論における合成問題は次のとおりです。明確に形式化された言語の観点から、設計されたオートマトンの動作 (オートマトンで表現されるイベント) の条件が記述されます。この場合、それぞれの書面条件に応じた方法を開発する必要があります。
1) 状態マシンによって変換された情報がこの条件を満たすような状態マシンが存在するかどうかを調べます。
2) はいの場合、そのような有限状態マシンの遷移関数が構築されるか、そのメモリ サイズが推定されます。
このような定式化における合成タスクの解決策は、記録から推移関数への移行に便利なアルゴリズムを備えたオートマトンの動作条件を記録するための便利な言語を事前に作成することを前提としています。
オートマトンの構造理論では、合成問題は、遷移関数によって与えられる有限オートマトンを実現する、特定のタイプの要素のチェーンを構築することにあります。この場合、通常、何らかの最適性基準 (要素の最小数など) を示し、最適なスキームを取得しようとします。
後で判明したように、これは、リレー接点回路に関連して以前に開発された方法と概念の一部が別のタイプの回路にも適用できることを意味します。
電子技術の発展に関連して、最も普及しているのは次のようなスキームです。 機能要素の (論理ネットワーク)。論理ネットワークの特殊なケースは、要素がニューロンと呼ばれる抽象ニューラル ネットワークです。
回路の種類と目的の情報の変換に応じて、多くの合成方法が開発されています (リレー デバイスの合成)。
有限状態マシン — 固定(動作中に増加できない)メモリ サイズを持つ制御システムの数学的モデル。
有限状態マシンの概念は、一連の制御システム (マルチループ リレー デバイスなど) の一般的な特性を特徴付ける数学的抽象概念です。このようなシステムはすべて、有限オートマトンの定義として自然に受け入れられる共通の特徴を持っています。
完成したすべてのオートマトンには、外部の影響や内部要素にさらされる入り口があります。入力要素と内部要素の両方について、それらが取り得る離散状態の数は固定されています。
入力要素と内部要素の状態の変化は離散的な瞬間に発生し、その間隔はティックと呼ばれます。テープの終わりの内部状態 (内部の状態) は、テープの最初の内部状態と入力の状態によって完全に決まります。
有限オートマトンの他のすべての定義、特に有限オートマトンが特定の時点でのオートマトンの内部状態に依存する出力を持つと仮定する定義は、この特性に帰着できます。
このような特性に関して、その入力と内部状態の性質は完全なオートマトンの記述とは無関係です。入力と状態の代わりに、ランダムな番号付けでその数値を確認するだけです。
ステート マシンは、その内部状態番号の、前の内部状態番号および前の入力状態番号への依存性が指定されている場合に設定されます。このようなタスクは、最終テーブルの形式にすることができます。
完全なオートマトンを定義するもう 1 つの一般的な方法は、いわゆる遷移図。入力状態は単に入力と呼ばれることが多く、内部状態は単に状態と呼ばれます。
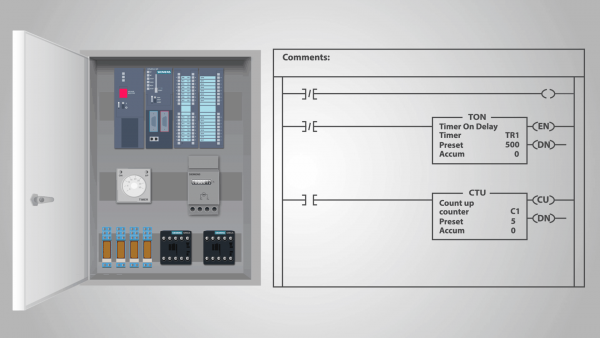
有限状態マシンは、技術デバイスと一部の生物学的システムの両方のモデルになることができます。第 1 のタイプのオートマトンは、たとえば、中継装置やさまざまな電子コンピュータです。 プログラマブルロジックコントローラー.
リレーデバイスの場合、入力状態の役割は、リレーデバイスの敏感な要素の状態の組み合わせによって果たされます(そのような状態の各組み合わせは「複雑な状態」であり、すべての敏感な要素を示すことによって特徴付けられます)特定の瞬間に持つこれらの離散状態)。同様に、中継デバイスの中間要素の状態の組み合わせは、内部状態として機能します。
プログラマブル ロジック コントローラー (PLC) は、スタンドアロン ステート マシンと呼ばれるリレー アクション デバイスの一例です。
実際、プログラムが PLC に入力され、コントローラーが計算を開始すると、外部の影響を受けることはなく、その後の各状態はその前の状態によって完全に決定されます。入力はすべてのクロック サイクルで同じ状態であると仮定できます。
逆に、唯一の可能な入力状態を持つ有限状態マシンは当然、自律型と呼ばれます。この場合、外部環境はその動作を制御する情報を持たないからです。
以下も参照してください。