AND、OR、NOT、AND-NOT、OR-NOT 論理ゲートとその真理値表

入力データに対して論理演算を実行するように設計された電気回路は、論理要素と呼ばれます。ここでは、入力データはさまざまなレベルの電圧の形式で表され、出力に対する論理演算の結果も、特定のレベルの電圧の形式で取得されます。

この場合、オペランドが渡されます。 二進数表記で — ロジック エレメントの入力は、基本的に入力データとして機能する高電圧または低電圧の形式で信号を受け取ります。したがって、高レベル電圧 (論理 1) はオペランドの真の値を意味し、低レベル電圧 0 (論理値 1) は偽の値を意味します。 1 - 真、0 - 偽。

論理要素 — 入力信号と出力信号間の特定の論理接続を実装する要素。論理要素は、コンピュータ論理回路、自動制御および管理のための個別回路を構築するために一般的に使用されます。すべてのタイプの論理要素は、その物理的性質に関係なく、入力信号と出力信号の離散値によって特徴付けられます。

論理ゲートには 1 つ以上の入力と 1 つまたは 2 つの (通常は反転された) 出力があります。論理要素の出力信号の「ゼロ」と「1」の値は、要素によって実行される論理関数と、再生される入力信号の「0」と「1」の値によって決まります。独立変数の役割。複雑な論理関数を構築するために使用できる基本的な論理関数があります。

要素の回路の配置、その電気的パラメータに応じて、入力と出力の論理レベル（高電圧レベルと低電圧レベル）は、高状態と低状態（真と偽）で同じ値を持ちます。

従来、論理要素は特別な無線コンポーネント、つまり集積回路の形で製造されてきました。結合、分離、否定、および加算モジュロ (AND、OR、NOT、排他的 OR) などの論理演算は、基本タイプの論理要素に対して実行される基本演算です。これらのタイプの論理ゲートをそれぞれ詳しく見てみましょう。

論理要素「AND」 — 接続、論理積、および AND

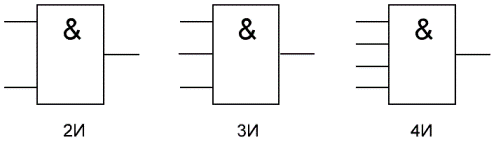
「AND」は、入力データの連結または論理積を実行する論理要素です。この要素には、2 ～ 8 個の入力 (2、3、4、および 8 個の入力を持つ製品で最も一般的な「AND」要素) と 1 つの出力を持つことができます。

異なる入力数を持つ論理要素«AND»のシンボルが図に示されています。本文では、1 つまたは別の数の入力を持つ論理要素 «And» は、«2I»、«4I» などとして指定されます。 — 2 つの入力を持つ要素「AND」、4 つの入力を持つ要素など。

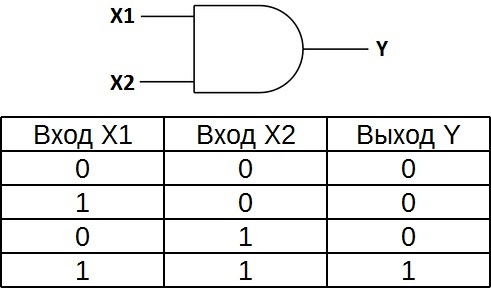
要素 2I の真理表は、論理 1 が最初の入力と 2 番目の入力の両方にある場合にのみ、要素の出力が論理 1 になることを示しています。他の 3 つの考えられるケースでは、出力はゼロになります。

西洋の図では、「And」要素のアイコンは入口が直線で出口が丸くなっています。内部図では、«&» 記号が付いた四角形。

OR 論理要素 - 論理和、論理和、OR

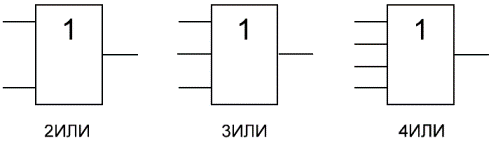
「OR」は、入力データに対して素または論理加算演算を実行する論理要素で、「AND」要素と同様に、2、3、4 などで生成されます。入力と 1 つの出力。異なる入力数を持つ論理要素«OR»のシンボルが図に示されています。これらの要素には、2OR、3OR、4OR などのラベルが付けられます。

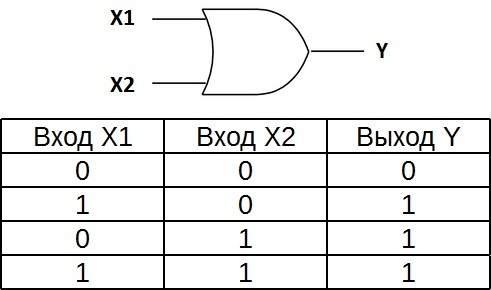
要素«2OR»の真理表は、出力における論理ユニットの出現には、論理ユニットが最初の入力上にある、または2番目の入力上にあるだけで十分であることを示しています。ロジックが同時に 2 つの入力にある場合、出力も 1 つになります。

西洋の図では、OR 要素には丸い入口点と丸い出口点があります。内部図では、«1» という記号が付いた四角形が表示されます。

論理ゲート«NO» — 否定、インバータ、NO

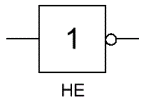
«NOT» は、入力データに対して論理否定演算を実行する論理要素です。出力が1つ、入力が1つだけのこの素子は、実際に入力信号を反転（反転）させるため、インバータとも呼ばれます。この図は、「NO」論理要素の従来の表記法を示しています。

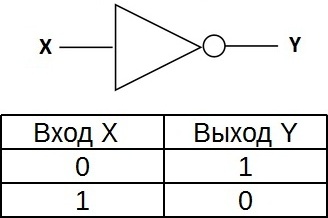
インバータの真理表は、入力の高電位が出力の低電位を与え、その逆も同様であることを示しています。

西洋の図では、要素«NO»のアイコンは、出口に円が付いた三角形の形状をしています。ビットチェーン上では、シンボル«1»が付いた四角形と、出力に円が付いています。

論理要素«AND-NOT» — 否定、NANDとの接続(論理積)

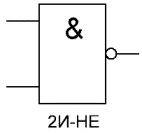
«AND-NOT» — 入力データの論理加算演算を実行し、その後論理否定演算を実行し、その結果が出力に供給される論理要素。つまり、基本的には AND 要素に NOT 要素を追加したものになります。図は論理要素«2I-NOT»の従来の表記法を示しています。

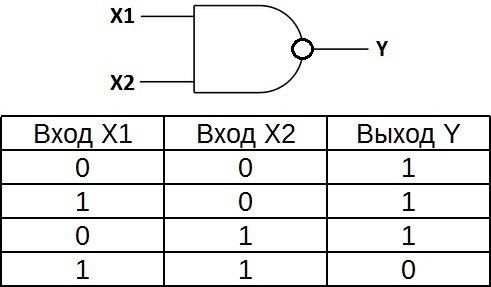
NAND 要素の真理値表は、AND 要素の真理値表の逆になります。 3 つのゼロと 1 つの代わりに、3 つの 1 と 0 があります。 NAND 素子は、この重要性を最初に指摘した数学者ヘンリー モリス シェーファーにちなんで、シェーファー素子とも呼ばれます。 論理演算 出口に丸があるだけで、「And」と指定されています。

論理要素 «OR-NOT» — 否定による論理和 (論理和)、NOR

«OR -NOT» — 入力データに対して論理加算の演算を実行し、次に論理否定の演算を実行し、その結果が出力に供給される論理要素です。言い換えれば、それは「OR」要素に「NOT」要素、つまりインバータが追加されたものです。図は、論理要素«2OR-NOT»の従来の表記法を示しています。

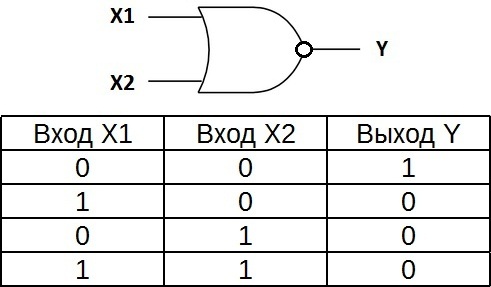
OR-NOT 要素の真理値表は、OR 要素の真理値表の逆になります。出力での高電位は 1 つの場合にのみ得られ、低電位が両方の入力に同時に適用されます。 «OR» として示され、反転を示す出力円のみが付きます。

論理ゲート«排他的OR» — 加算法2、XOR

「排他的 OR」 — 入力データを 2 を法として加算する論理演算を実行する論理要素で、2 つの入力と 1 つの出力があります。これらの要素は制御スキームでよく使用されます。図はこの元素の記号を示しています。

西洋のスキームでは、入り口の側面に追加の湾曲したバーを備えた«OR»として、国内のスキームでは«OR»として、«1»の代わりにのみ«= 1»と書かれます。

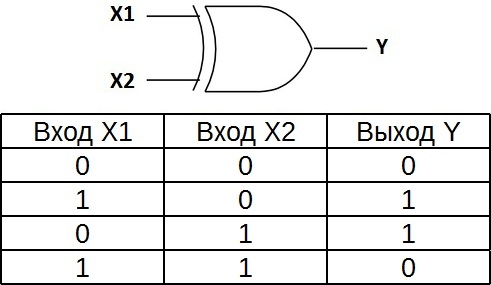
この論理要素は「不等式」とも呼ばれます。入力信号が等しくない場合（一方が 1、もう一方がゼロ、または一方がゼロともう一方が 1）にのみ、出力に高電圧レベルが発生します。たとえ入力に同時に 2 つの信号があったとしても、出力はゼロであること — これが«OR»との違いです。これらの論理要素は加算器で広く使用されています。