非線形電気回路
電気回路における非線形要素の目的
V 電気回路 受動的な要素が含まれる場合があります。 電気抵抗 これは基本的に電流またはストレスに依存するため、電流は電圧に直接比例しません。このような素子とそれが入る電気回路を非線形素子と呼びます。
非線形要素は、線形回路では達成できない特性 (電圧または電流の安定化、DC 増幅など) を電気回路に与えます。それらは制御不可能であり、制御されています...最初の - バイポーラ - は制御要因の影響を受けずに動作するように設計されています (半導体サーミスタやダイオード)。2 つ目 - 多極 - は制御要因がそれらに作用する場合に使用されます (トランジスタ)およびサイリスタ)。
非線形素子の電流電圧特性
非線形素子の電気的特性は、電流の電圧依存性を実験的に得た電流電圧特性I(U)のグラフであり、計算に便利な近似的な経験式が作られることもあります。
制御されていない非線形要素は単一の電流電圧特性を持ち、制御された非線形要素はパラメータが制御因子である一連の特性を持ちます。
線形素子は電気抵抗が一定であるため、その電流電圧特性は原点を通る直線になります(図1a)。
非線形の電流電圧特性は形状が異なり、座標軸に対して対称と非対称に分けられます(図1、b、c)。
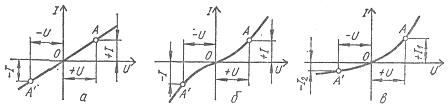
米。 1. 受動素子の電流電圧特性: a — 線形、b — 非線形対称、c — 非線形非対称
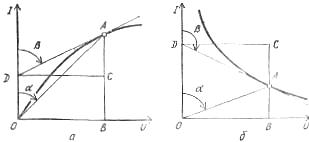
米。 2. 電流電圧特性の各セクションにおける非線形素子の静微分抵抗を決定するためのグラフ: a - 上昇、b - 立ち下がり
電流電圧特性が対称な非線形素子や対称素子の場合、電圧の方向が変化しても電流値は変化しません(図1、b)、電圧が非対称な非線形素子の場合は、 -電流特性、または非対称要素の場合、電圧の絶対値が同じで反対方向に向けられると、電流は異なります(図1、c)。したがって、非線形対称素子はDCおよびAC回路で使用され、非線形不平衡素子は原則としてAC回路でACをDC電流に変換するために使用されます。
非線形要素の特徴
各非線形要素について、電流-電圧特性の特定の点、たとえば点 A に対応する静抵抗が区別されます。
Rst = U / I = muOB / miBA = mr tgα
そしてそのための微分抵抗。同じ点 A は次の式で求められます。
Rdiff = dU / dI = muDC / miCA = mr tgβ、
ここで、mi、mi、sir - それぞれ、電圧、電流、抵抗のスケールです。
静的抵抗は定電流モードでの非線形要素の特性を特徴づけ、微分抵抗は定常状態値からの電流の小さな偏差を特徴づけます。電流-電圧特性は、ある点から別の点に移るときに両方とも変化します。最初の点は常に正で、2 番目の変数は特性の上昇部分では正で、下降部分では負になります。
非線形要素は、静伝導率 Gst および微分伝導率 G の逆数値によっても特徴付けられます。異なるパラメーターまたは無次元パラメーター —
相対抵抗:
Kr = — (R 差 /Rst)
または相対導電率:
Kg = — (G 差 / Gst)
線形要素では Kr と Kilogram のパラメータが 1 に等しく、非線形要素ではパラメータ Kr と Kilogram が 1 と異なり、1 から離れるほど電気回路の非線形性が現れます。
 非線形電気回路の計算
非線形電気回路の計算
非線形電気回路は、以下に基づいてグラフィックおよび分析的に計算されます。 キルヒホッフの法則 交流を直流に変換する交流回路の個々の要素のボルトアンペア特性。
電流-電圧特性 Iz (U1) および Iz (U2) を持つ 2 つの直列接続された非線形抵抗 R1 および R2 を備えた電気回路をグラフで計算する場合、回路全体の電流-電圧特性 Iz (U) を構築します。ここで、U = U1 + U2、その点の横座標は、同じ縦軸を持つ非線形抵抗器の電流電圧特性の点の横座標を合計することによって求められます(図3、a、b)。
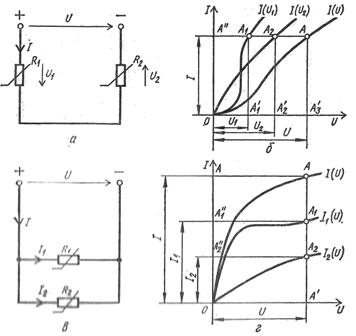
米。 3. 非線形電気回路の図と特性: a — 非線形抵抗器の直列接続の回路、b — 個々の素子と直列回路の電圧-電流特性、c — 非線形抵抗器の並列接続のスキーム、d — 個々の要素と並列回路のボルトアンペア特性。
この曲線の存在により、電圧 U から電流 Az と、抵抗器の端子の電圧 U1 および U2 を求めることができます。
同様に、2つの抵抗を並列に接続した電気回路の計算を行います。電流-電圧特性 I1 (U) および Az2 (U) を持つ R1 および R2。回路全体の電流-電圧特性 Az(U) が構築されます。ここで、Az = I1+I2 は、所定の電圧を使用します。 U、電流 Az 、I1、I2 (oriz. 3、c、d) を求めます。
非線形電気回路を計算するための解析方法は、対応する数学関数の方程式による非線形要素の電圧特性の表現に基づいており、電気回路に必要な状態方程式を作成することができます。 。このような非線形方程式の解法は大きな困難を引き起こすことが多いため、非線形素子の電流電圧特性の動作区間を直線化できる場合には非線形回路を解析的に計算する手法が便利です。これにより、回路の電気的状態を線形方程式で記述することができるため、問題を解くのが難しくなります。
電気工学の基礎:

