回路トポロジー - 基本概念

電気回路は、電流が流れる一連のデバイス (要素) とそれらの接続ワイヤです。電気回路のすべての要素は共通しています 受動的と能動的で.

アクティブ要素は、さまざまな種類のエネルギー (機械、化学、光など) を電気エネルギーに変換します。受動デバイスでは、電気エネルギーが他の種類のエネルギーに変換されます。能動的な要素はソースと呼ばれ、受動的な要素はコンシューマまたはレシーバと呼ばれます。

回路理論では、電気要素の理想化されたモデルが考慮されます。これにより、要素の説明ができるだけ簡単になります。より複雑な実際の要素は、理想化された要素のセットからモデル化されます。

電気回路の主な受動素子は、レジスタ（抵抗素子）、インダクタ（誘導素子）、コンデンサ（容量素子）です。要素は電気回路に取り付けられ、特定の値と形状の電圧と電流を生成します (—を参照) 電気回路とその要素).

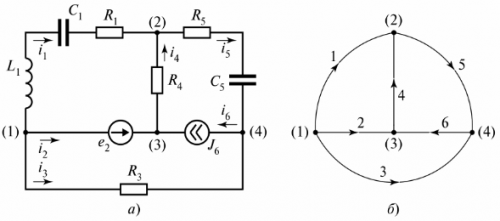
電気回路は分岐とノードで構成されます。 ブランチ — これは、同じ電流が流れる電気回路（回路）の一部です。 結び目 — 3 つ以上の分岐の接続。電気回路図では、ノードは点で示されます (図 1)。

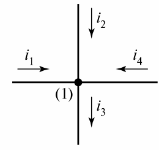
米。 1. ダイアグラム内のノードを定義します

必要に応じて、図のノードには左から右、上から下の順に番号が付けられます。

図では。図２は、電流ｉＣが流れる抵抗性と容量性の分岐を示している。

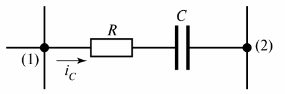
米。 2. 抵抗-容量性分岐

ブランチの別の定義を与えることもできます。それは、2 つの隣接するノード (図 2 のノード (1) と (2)) の間の回路のセクションです。

鎖 電気回路内に閉じた経路はありますか。回路は、抵抗が無限大に等しい条件付き分岐を含む、任意の分岐によって閉じることができます。

図では。図３は、３つの分岐からなる分岐電気回路を示す。

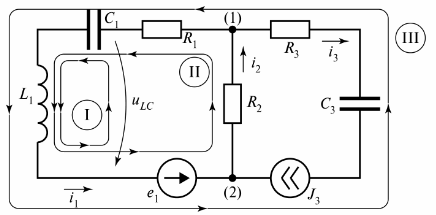
米。 3. 2回路の電気回路

この図には 3 つの回路が示されており、回路 I は無限抵抗の分岐によって閉じられています。この分岐は電圧 tiLC として示されます。

図の回路の場合、 3 実分岐または条件分岐によって閉じられる多数のループを構成することは可能ですが、電気ノイズの計算には「独立ループ」の概念が使用されます。独立した回路ループの数は、計算に必要な最小値として常に設定されます。

独立した回路は常に閉じていますが、抵抗が無限大に等しくない分岐があり、各独立した回路には他の回路に含まれない少なくとも 1 つの分岐が含まれます。複雑な電気回路の場合は、回路図を使用して独立した回路の数を決定できます。

回路図上では 回路の条件付き表現が呼び出され、各分岐が線分に置き換えられます。ブランチ内のアイテムは表示されません。例えば、図１では、図４に分岐回路とその回路図を示す。

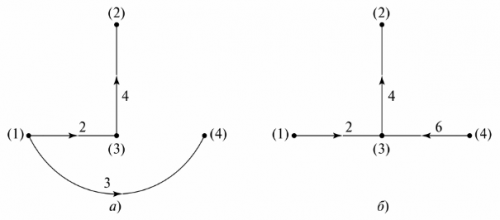
米。 4. 分岐電気回路: a — 回路図、b — 図

ダイアグラムを作成するには、ノード上の要素を指定せずに、ノード間を支線で接続する必要があります。枝には番号が付けられ、枝を流れる電流の方向が矢印で示されます。グラフ自体には物理的な意味はありませんが、独立した等高線の数と種類を決定するために使用できます。そのために「グラフィックツリー」が用意されています。

グラフィックツリー これは、閉ループが生じないようにノードが分岐によって接続されている回路のグラフを表します。グラフィカル ツリーを表示するには、いくつかのオプションがある場合があります。図では。図５は、図４の回路の２つの可能な選択肢を示す。 4.

米。 5. スキームのグラフィックツリー

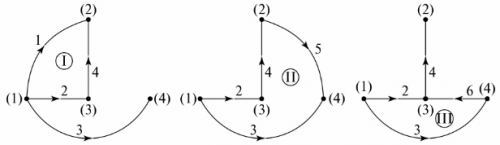
グラフ ツリー内の欠落している分岐の数は、回路の独立したループの数に等しい。この例では、これらは 3 つの分岐、3 つの独立したループです。グラフツリー上のノードを、グラフツリー上で指定されていない枝に順次接続することで、独立したループの構成を得ることができる。たとえば、図のグラフツリーの場合、独立した輪郭を図5に示します。 6.

米。 6. グラフツリーによる独立した等高線の決定

回路を計算するために独立した回路を構成するオプションの選択は、回路解析中に実行されます。計算ができるだけ簡単になるように、そのような等高線を選択する必要があります。システム内の従属方程式の数は最小限です。

トポロジー方程式は回路内の電圧と電流の間の関係を確立し、方程式の数と種類は分岐に含まれる要素には依存しません。トポロジカル方程式には、以下から構成される方程式が含まれます。 キルヒホッフの法則によると.