単一電源の非分岐および分岐リニア電気回路
 多数の受動素子が e のソースと一緒にある場合。等c. 電気回路を形成する場合、それらの相互接続はさまざまな方法で行うことができます。このような接続には次のような代表的な方式があります。
多数の受動素子が e のソースと一緒にある場合。等c. 電気回路を形成する場合、それらの相互接続はさまざまな方法で行うことができます。このような接続には次のような代表的な方式があります。
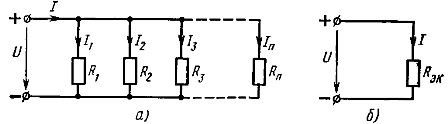
エレメントの直列接続 最も単純な接続です。この接続では、回路のすべての要素に同じ電流が流れます。この方式によれば、回路のすべての受動素子を接続して分岐のない単回路にするか(図1、a)、多回路回路の一部の素子のみを接続することができます。接続されています。
同じ電流 I が流れる n 個の素子が直列に接続されている場合、回路の端子の電圧は、直列に接続されている n 個の素子での電圧降下の合計に等しくなります。
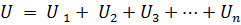
または:
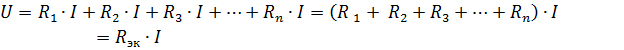
ここで、Rek は等価回路抵抗です。
したがって、直列に接続された受動素子の等価抵抗は、これらの素子の抵抗の合計に等しくなります。1、a) 等価抵抗 Rek を持つ 1 つの要素からなる等価回路を表すことができます (図 1、b)。
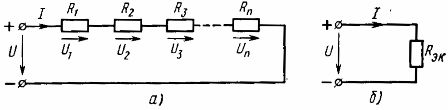
米。 1. 線状素子の直列接続方式(a)とその等価方式(b)
与えられた電源電圧と素子の抵抗で直列に接続された素子を含む回路を計算する場合、回路内の電流はオームの法則に従って計算されます。
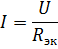
k番目の要素の電圧降下
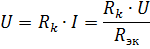
は、この要素の抵抗だけでなく、等価抵抗 Rek、つまり回路の他の要素の抵抗にも依存します。これは、要素の直列接続の重大な欠点です。限定的なケースでは、回路のいずれかの要素の抵抗が無限大に等しくなると (開回路)、回路のすべての要素の電流はゼロになります。
直列に接続すると、回路のすべての要素の電流が同じになるため、要素の電圧降下の比率はこれらの要素の抵抗の比率に等しくなります。
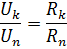
要素の並列接続 — これは、回路のすべての要素に同じ電圧が印加される接続です。並列接続方式によれば、回路のすべての受動素子(図2、a)またはその一部のみを接続できます。並列接続された各要素は個別の分岐を形成します。したがって、図に示す素子を並列接続した回路は次のようになります。 2、a、単純な回路(ノードが 2 つしかないため)ですが、同時に分岐します。
米。 2. 線状要素の並列接続方式 (a) とその等価方式 (b)
各並列分岐では、電流
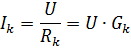
ここで、Gk は k 番目のブランチの導電率です。
から キルヒホッフの第一法則
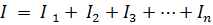
また
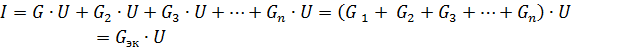
ここで、Gec は等価回路コンダクタンスです。
したがって、受動素子が並列に接続されている場合、それらの等価コンダクタンスは、これらの素子のコンダクタンスの合計に等しくなります。等価コンダクタンスは、常に並列分岐のどの部分のコンダクタンスよりも大きくなります。等価導電率 GEK は等価抵抗 Rek = 1 / Gek に対応します。
すると、図のような等価回路になります。 2のaは図のような形になります。 2, b. 素子が並列接続されている回路の分岐していない部分の電流は、オームの法則に従ってこの回路から求めることができます。
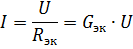
したがって、電源電圧が一定の場合、並列接続する素子の数が増えると(等価導電率が増加し)、回路の分岐されていない部分の電流(電源電流)が増加します。
式から
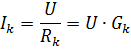
各分岐の電流はその分岐のコンダクタンスのみに依存し、他の分岐のコンダクタンスには依存しないことがわかります。並列分岐モードが互いに独立していることは、受動素子の並列接続の重要な利点です。産業用設備では、ほとんどの場合、受電器の並列接続が使用されます。最もわかりやすい例は、照明用の電球の組み込みです。
並列接続ではすべての要素に同じ電圧が印加され、各分岐の電流はその分岐のコンダクタンスに比例するため、並列分岐の電流の比はこれらの分岐のコンダクタンスの比に等しいか、または反比例します。それらの抵抗の比に:
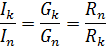
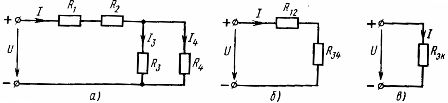
要素の混合接続は、直列接続と並列接続の組み合わせです。このようなチェーンには、異なる数のノードとブランチを含めることができます。混合接続の例を図に示します (図 3、a)。
米。 3. 線形要素の混合接続のスキーム (a) とその等価なスキーム (b、c)。
このような回路を計算するには、回路の直列接続のみまたは並列接続のみの部分の等価抵抗を逐次求める必要があります。考慮した回路では、抵抗 R1 および R2 を持つ要素の直列接続と、抵抗 R3 および R4 を持つ要素の並列接続があります。事前に取得した回路要素の直列および並列接続のパラメータ間の関係を使用して、実際の電気回路を等価回路に置き換えることができます。
直列接続した素子の等価抵抗
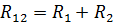
並列接続要素 R3 と R4 の等価抵抗
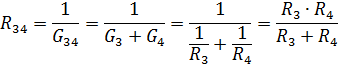
素子R12とR34の抵抗による等価回路を図に示します。 3、b. R12 と R34 のこの直列接続の場合、等価抵抗は次のようになります。
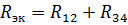
対応する等価回路を図に示します。 2、b.この回路の電流を求めてみましょう。
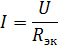
これらは、実際の回路の供給電流と要素 R1 および R2 の電流です。電流 I3 と I4 を計算するには、回路の抵抗 R34 のある部分の電圧を決定します (図 3、b)。
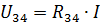
次に、電流 I3 と I4 はオームの法則に従って求められます。
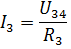
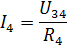
同様の方法で、受動素子を混合接続した他の多くの電気回路を計算できます。
e. 多数の回路とソースを含む複雑な回路の場合。等c. このような等価変換は常に実行できるわけではありません。他の方法で計算されます。