直並列接続時の抵抗値の計算

概念と公式

直並列または混合接続は、3 つ以上の抵抗の複雑な接続です。混合接続の結果として得られる抵抗は、直列および並列接続の抵抗を計算する式を使用して段階的に計算されます。

の例

1. 図の図に従って、3 つの抵抗の直並列接続を計算します。 1.

まず、並列接続された抵抗 r2 と r3 を結果の抵抗 r (2-3) に置き換えます。

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6.6 オーム。

回路全体の抵抗は、r = r1 + r (2-3) = 5 + 6.6 = 11.6 オームとなります。

米。 1.

2. 開路と閉路の回路（図2）にはどのような電流が流れるか ナイフスイッチ Ｐ？どちらの場合でも、抵抗 r2 の両端の電圧はどのように変化しますか?

米。 2.

a) スイッチが開いています。直列接続された抵抗r1とr2の合成抵抗

r(1-2) = r1 + r2 = 25 オーム。

電流 I (1-2) = U / r (1-2) = 100/25 = 4 A。

抵抗r2の両端の電圧降下

U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V。

b) スイッチが閉じている。並列接続された抵抗r1とr3の合成抵抗

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6.6 オーム。

回路全体の合計抵抗は、r = r (1-3) + r2 = 6.6 + 5 = 11.6 オームです。

電流 I = U / r = 100 / 11.6 = 8.62 A。

この場合の抵抗 r2 での電圧降下は、U2 = I ∙ r2 = 8.62 ∙ 5 = 43.25 V に等しくなります。

2 番目のケースでは、並列抵抗 R3 を接続した結果、電流が増加しました。より多くの電流がより多くの電流を生み出す 電圧降下 抵抗r2で。

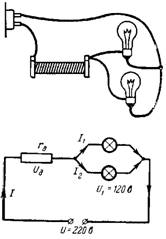
3. どうあるべきか 追加の抵抗 rd、つまり、電圧 120 V、電流 0.2 A で並列接続された 2 つのランプを電圧 U = 220 V のネットワークに接続できるようになります (図 3)。

米。 3.

ランプの電圧は 120 V である必要があります。残りの電圧 (100 V) は追加の抵抗 rd にかかります。 2 つのランプの電流 I = 0.4 A が抵抗 rd を流れます。

オームの法則によると、rd = Ud / I = 100 / 0.4 = 250 オームです。

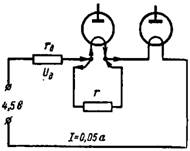
4. 1.2 V のフィラメントと 0.025 A および 0.05 A のフィラメント電流を備えた電子ランプが 4.5 V の DC 電源に直列に接続されています。追加の抵抗 rd および 並列抵抗（シャント） フィラメント電流が低いランプに接続する必要がありますか (図 4)。

米。 4.

回路内の抵抗は、2 番目のランプのフィラメント電流が I = 0.05 A 流れるように選択する必要があります。電子ランプのフィラメントにかかる電圧は 1.2 + 1.2 = 2.4 V になります。この値をバッテリー電圧から引くと、次のようになります。追加の抵抗 rd での電圧降下の値を取得します: Ud = 4.5-2.4 = 2.1 V。

したがって、追加の抵抗は rd = (Ud) / I = 2.1 / 0.05 = 42 オームとなります。

最初の真空管のフィラメントには 0.05 A のフィラメント電流が流れてはなりません。この電流の半分 (0.05-0.025 = 0.025 A) はシャント r を通過する必要があります。シャント電圧はランプのフィラメントと同じです。したがって、シャント抵抗は、r = 1.2 / 0.025 = 48 オームとなります。

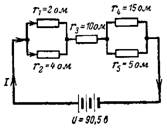
5. 図の回路で得られる回路抵抗とそこに流れる電流はいくらですか。 5?

米。 5.

まず、並列接続された抵抗の結果として得られる抵抗を決定しましょう。

r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1.3 オーム;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3.75 オーム。

結果として生じる回路抵抗は次のようになります。

r = r (1-2) + r3 + r (4-5) = 1.3 + 10 + 3.75 = 15.05 オーム。

電圧 U = 90.5 V での結果の電流

I = U / r = 90.5 / 15.05 = 6 A。

6. 図の回路における複雑な直並列接続の結果として生じる抵抗を計算します。 6. 結果として得られる電流 I、電流 I4、および抵抗 r1 の両端の電圧降下を計算します。

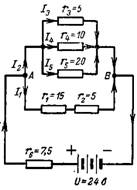
米。 6.

並列接続された抵抗の合成コンダクタンス

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 シム;

r (3-4-5) = 20/7 = 2.85 オーム。

r1 と r2 の回路抵抗は次のとおりです。

r (1-2) = r1 + r2 = 15 + 5 = 20 オーム。

結果として得られる点 A と点 B の間の導電率と抵抗はそれぞれ等しい: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2.5 オーム。

回路全体の抵抗は、r = rAB + r6 = 2.5 + 7.5 = 10 オームとなります。

結果として得られる電流は、I = U / r = 24/10 = 2.4 A となります。

点AとBの間の電圧は、電源電圧Uから抵抗r6の両端の電圧降下を引いたものに等しくなります。

UAB = U-1 ∙ r6 = 24-(2.4 ∙ 7.5) = 6V。

抵抗 r4 はこの電圧に接続されているため、抵抗 r4 を流れる電流は次のようになります。

I4 = UAB / r4 = 6/10 = 0.6A。

抵抗 r1 と r2 には共通の電圧降下 UAB があるため、r1 を流れる電流は次のようになります。

I1 = UAB / r (1-2) = 6/20 = 0.3 A。

抵抗r1の両端の電圧降下

Ur1 = I1 ∙ r1 = 0.3 ∙ 15 = 4.5 V。

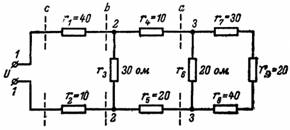
7. 図の回路で得られる抵抗と電流はいくらですか。 7 電源電圧が U = 220 V の場合?

米。 7。

ノード 3 と 3 の右側にある回路から始めます。抵抗 r7、r8、r9 は直列に接続されているため、

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 オーム。

抵抗 r6 がこの抵抗と並列に接続されているため、結果としてノード 3 と 3 に抵抗が生じます (セクション a)。

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16.36 オーム。

抵抗 r4 と r5 は抵抗 ra と直列に接続されています。

r (4-5-a) = 10 + 20 + 16.36 = 46.36 オーム。

ノード 2 と 2 の合成抵抗 (セクション b)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46.36 ∙ 30) / (46.36 + 30) = 1390.8 / 76、36 = 18.28 オーム。

回路全体の抵抗は、r = r1 + rb + r2 = 40 + 18.28 + 10 = 68.28 オームとなります。

結果として生じる電流は、I = U / r = 220 / 68.28 = 3.8 A となります。