単相交流

交流電流の取得

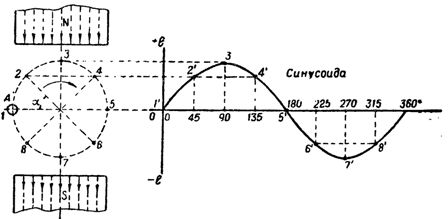
磁石の 2 つの極によって形成される磁束の中でワイヤ A が時計回りに回転すると (図 1)、ワイヤが磁力線を横切るときに e. d が誘起されます。値が式によって決定される s

E = Blvsinα、

ここで、B は T 単位の磁気誘導、l はワイヤの長さ (m)、v はワイヤの速度 (m / s)、α - ワイヤが磁力線と交差する角度です。

この場合の B、I、v が一定のままであるとすると、誘導される e が決まります。等c. は、ワイヤが磁場と交差する角度 α にのみ依存します。したがって、点 1 では、ワイヤが磁力線に沿って移動するとき、誘導起電力の値は次のようになります。等ワイヤが点 3 oe に移動すると、p はゼロになります。等v. 力線は導体によってそれらに垂直な方向に交差し、最後に例えば力線が交差するため、最も重要になります。等v. ワイヤをポイント 5 に移動すると、再びゼロになります。

米。 1. 誘導された e を変更します。等pp. 磁場中で回転するワイヤー内

ワイヤが角度 α = 45 ° で力線と交差する中間点 2 と 4 では、誘導起電力の値は次のようになります。等したがって、ワイヤが点 1 から点 5 に、つまり 180 °回転すると、誘導される e. c. は点 3 よりも小さくなります。等v. ゼロから最大値に変化し、再びゼロに戻ります。

ワイヤ A をさらに 180°回転させると (点 6、7、8、1 を介して)、誘導される e の変化の性質が変化することは明らかです。等p.は同じですが、ワイヤがもう一方の極の下ですでに磁力線を横切るため、その方向は反対に変わります。これは、磁力線を反対の最初の方向に横切ることと同じです。

したがって、ワイヤーが 360 ° 回転すると、誘導される e.等v. 大きさが常に変化するだけでなく、方向も 2 回変わります。

ワイヤーがある程度の抵抗まで閉じられると、ワイヤーが表示されます。 電気、サイズや方向も異なります。

大きさと方向が連続的に変化する電流を交流といいます。

正弦波とは何ですか?

変更の性質 ｅ．等より明確にするために、ワイヤーの 1 ターン分の (電流) が曲線を使用してグラフで表されています。 eの値以来。等c. sinα に比例し、特定の角度を設定すると、テーブルを使用して各角度のサインの値を決定し、適切なスケールで e の変化に対する曲線を構築することができます。等c. これを行うには、水平軸にワイヤの回転角度を設定し、垂直軸に適切なスケールで誘導 e を設定します。等と

前に図に示した場合。1 点を滑らかな曲線で結ぶと、誘発された e の変化の大きさと性質がわかります。等磁場内の導体の任意の位置における（電流）。誘導された e の値が次のとおりであるという事実のため。等p. はいつでも、図に示すワイヤが磁場を横切る角度の正弦によって決まります。 1 の曲線は正弦波と呼ばれ、e.等s. — 正弦波。

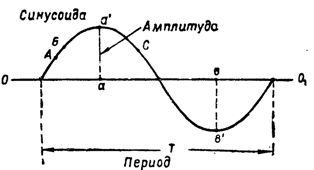
米。 2. 正弦波とその特性値

調査した変更点 e.等c. 正弦波は、磁場中での 360 ° の角度でのワイヤの回転に対応します。ワイヤーが次の 360 ° 回転すると、誘導される e が変化します。等s.（および電流）は再び正弦波で表示されます。つまり、周期的に繰り返されます。

したがって、これによって引き起こされるｅ．等c. 電流は正弦波交流と呼ばれます... 閉じた外部回路が存在する場合、ワイヤ A の端で測定できる電圧も正弦波的に変化することは明らかです。

磁束の中で導線を回転させることによって得られる交流、またはコイル内に接続された導線系を単相交流といいます。

正弦波交流はテクノロジーで最も広く使用されています。ただし、正弦の法則に従って変化しない交流も存在します。このような交流は非正弦波と呼ばれます。

以下も参照してください。 交流とは何か、直流とどう違うのか

単相交流の振幅、周期、周波数

現在の強さ、正弦波に沿って変化し、連続的に変化します。したがって、点 A (図 2) での電流が 3a に等しい場合、点 B ではすでに電流は大きくなります。正弦波上の他の点、たとえば点 C では、電流は新しい値になります。

電流が正弦波状に変化するとき、ある時刻における電流の強さを瞬時電流値といいます。

単相交流電流の最大瞬間値は、正弦波振幅に沿って変化するときに呼び出されます。ワイヤを 1 回巻くと、電流が振幅値の 2 倍に達することが簡単にわかります。 aa ' の値の 1 つは正で、001 軸から上に描画され、もう 1 つの bv ' は負で、軸から下に描画されます。

eが誘導される時間。等（または現在の力）変化のサイクル全体、いわゆる月次サイクル T を通過します（図 2）。通常、期間は秒単位で測定されます。

周期の逆数を周波数(f)といいます。言い換えると、 交流周波数 は単位時間あたりの期間の数です。つまり、数秒で。したがって、たとえば、1秒以内の交流が同じ値と方向を10回仮定した場合、そのような交流の周波数は1秒あたり10周期になります。

周波数を測定するには、1 秒あたりの周期数の代わりに、ヘルツ (hertz) と呼ばれる単位が使用されます。 1 ヘルツの周波数は 1 lps/秒の周波数と同じです。高周波を測定する場合、ヘルツの 1000 倍、つまり 1000 倍の単位を使用すると便利です。キロヘルツ (kHz)、またはヘルツの 1,000,000 倍、メガヘルツ (mhz)。

技術で使用される交流は、周波数に応じて低周波電流と高周波電流に分類できます。

AC実効値

ワイヤーに直流電流を流すとワイヤーが加熱されます。ワイヤーに交流電流を流すとワイヤーも発熱します。交流の方向は常に変化しますが、熱の放出はワイヤ内の電流の方向にまったく依存しないため、これは理解できます。

電球に交流を流すとフィラメントが光ります。標準的な交流周波数 50 Hz では、回路内の電流がゼロになると熱慣性がある白熱電球のフィラメントが冷却する時間がないため、光のちらつきはありません。照明に周波数 50 Hz 未満の交流を使用することは、電球の強度に不快で目を疲れさせる変動が現れるため、現在では望ましくありません。

直流のアナロジーを続けると、ワイヤを流れる交流によってその周囲に電流が発生すると予想できます。 磁場。実際には、交流は磁界を生成しませんが、生成される磁界の方向と大きさも変化するためです。

交流電流は、大きさと方向 NS の両方が常に変化します。当然のことながら、変数 T をどのように測定するか、および正弦波に沿って変化するときのその値がどのような動作を引き起こすものとして解釈されるべきかという疑問が生じます。

C この目的のために、交流は、それが生み出す作用の観点から直流と比較され、その値は実験中変化しません。

定抵抗10Aの電線に直流電流が流れ、電線の温度が50℃に加熱されたとします。ここで、同じワイヤに直流ではなく交流を流し、ワイヤも50°の温度に加熱されるようにその値を選択します（たとえば加減抵抗器で動作します）。この場合、交流の作用は直流の作用と等しいと言えます。

どちらの場合もワイヤを同じ温度に加熱すると、単位時間内に交流が直流と同じ量の熱をワイヤ内で放出することがわかります。

直流電流と同じ大きさの直流電流と同じ量の熱を単位時間当たり所定の抵抗で放出する交流正弦波電流。この電流値は実効値 (Id) または交流の実効値と呼ばれます。したがって、この例では、交流の実効値は 10 A になります...この場合、最大 (ピーク) 電流値は大きさが平均値を超えます。

経験と計算によれば、交流の実効値はその振幅値よりも√2（1.41）倍小さいことがわかります。したがって、電流のピーク値がわかっている場合、電流 Id の実効値は、電流 Ia の振幅を√2 で割ることによって決定できます。つまり、Id = Aza/√2

逆に、電流の実効値がわかっている場合は、電流のピーク値を計算できます。すなわち、Ia = Azd√2

同じ関係が e の振幅と rms 値にも当てはまります。等v. および電圧: 単位 = Ea /√2、Ud = Uа/√2

測定器は実際の値を示すことが多いため、表記する場合、通常、インデックス «d» は省略されますが、これを忘れないでください。

AC回路のインピーダンス

インダクタンスとキャパシタンスの消費装置が AC 回路に接続されている場合、アクティブとリアクタンスの両方を考慮する必要があります (リアクタンスはコンデンサがオンまたはオンのときに発生します)。 AC回路のチョーク）。したがって、このような需要家に流れる電流を求める場合は、電源電圧を回路（需要家）のインピーダンスで割る必要があります。

単相交流回路のインピーダンス (Z) は、次の式で求められます。

Z = √(R2 + (ωL — 1 / ωC)2

ここで、R は回路のアクティブ抵抗 (オーム)、L は回路のインダクタンス (ヘンリー)、C は回路 (コンデンサ) の静電容量 (ファラッド)、ω - 交流の角周波数です。

R、L、C の 3 つの値、またはそれらの一部のみを考慮する必要がある交流回路では、さまざまな消費者が使用されます。同時に、交流の角周波数を考慮する必要があります。

一部のユーザーでは、対応するコーナー周波数値で R と L の値のみを考慮することができます（たとえば、AC 周波数 50 Hz では）。 ソレノイドコイル あるいは、発電機巻線には能動抵抗と誘導抵抗が含まれているとしか考えられません。つまり、この場合の静電容量は無視できることになります。このようなユーザーの AC インピーダンスは、次の式で計算できます。

Z = √(R2 + ω2L2)

このようなコイルや交流用のコイルを同電圧の直流に接続すると、コイルに非常に大きな電流が流れ、発熱が大きくなり、コイルの絶縁が損傷する可能性があります。逆に、直流回路で動作するように設計されたコイルを同じ電圧の交流回路に接続すると、微小な電流が流れ、このコイルを使用した機器は必要な動作をしません。

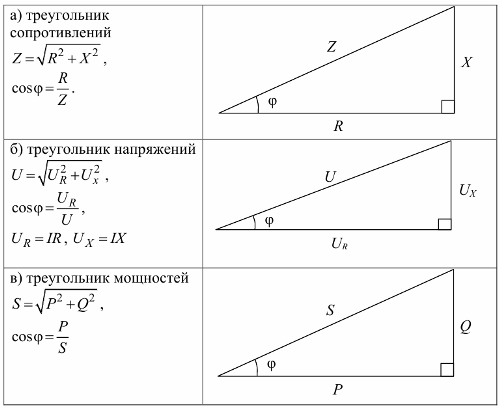
三角抵抗、三角電圧、電力三角: