電気工学の基本法則
オームの法則 (ドイツの物理学者 G. オーム (1787-1854) にちなんで命名) は、電気抵抗の単位です。表記オーム。オームは、その両端間のワイヤの抵抗です。 アンペア数 1 A の場合、1 V の電圧が発生します。電気抵抗の支配方程式は R = U / I です。
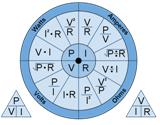
オームの法則は電気回路を計算する際に無視できない電気工学の基本法則です。導体間の電圧降下、その抵抗、電流の強さの関係は、頂点に U、I、R の記号がある三角形の形で簡単に覚えられます。
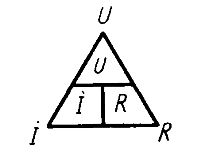
オームの法則
ジュール・レンツの法則 (イギリスの物理学者 J.P. ジュールとロシアの物理学者 E.H. レンツにちなんで命名) — 特徴づける法則 電流の熱効果.
法則によれば、直流電流が導体を通過するときに導体に放出される熱量 Q (ジュール) は、電流の強さ I (アンペア) に依存します。 配線抵抗 R (オーム単位) とその通過時間 t (秒単位): Q = I2Rt。
電気エネルギーの熱への変換は、電気炉やさまざまな電気加熱装置で広く使用されています。電気機械や装置における同様の影響は、不注意によるエネルギーの浪費 (エネルギーの損失と効率の低下) につながります。これらのデバイスの発熱の原因となる熱により、負荷が制限されます。過負荷がかかると、温度上昇により絶縁が損傷したり、ユニットの寿命が短くなる可能性があります。
キルヒホッフの法則 (ドイツの物理学者 G.R. キルヒホッフ (1824-1887) にちなんで命名) — 電気回路の 2 つの基本法則。第 1 法則は、接合点でノードに向かう電流の合計 (正) とノードから離れる方向に向かう電流の合計 (負) の間の関係を確立します。
ワイヤの分岐 (ノード) の各点で収束する電流 In の代数的合計はゼロに等しくなります。 SUMM (In) = 0。たとえば、ノード A の場合、次のように記述できます: I1 + I2 = I3 + I4 または I1 + I2 — I3 — I4 = 0。
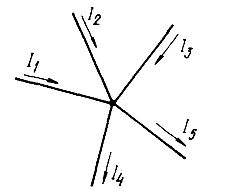
現在のノード
第 2 法則は、起電力の合計と電気回路の閉回路抵抗での電圧降下の合計との関係を確立します。ループの流れの任意に選択された方向と一致する電流は正とみなされ、一致しない電流は負とみなされます。
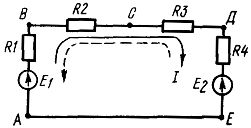
現在のサイクル
電気回路の各回路内のすべての電圧源の起電力の瞬時値の代数和は、同じ回路のすべての抵抗における電圧降下の瞬時値の代数和に等しい SUMM (En) = SUMM (InRn)。方程式の左側の SUMM (InRn) を並べ替えると、 SUMM (En) — SUMM (InRn) = 0 が得られます。 電気回路の閉回路のすべての要素の瞬時電圧の値の代数和はゼロに等しい。
完全な現在法則 電磁場の基本法則の 1 つ。それは、磁力と表面を通過する電流量との関係を確立します。総電流は、閉ループで囲まれた表面を通過する電流の代数和として理解されます。
ループに沿った磁化力は、このループで囲まれた表面を通過する総電流に等しくなります。一般に、磁力線の異なる部分の磁場の強さは異なる値を持つ可能性があり、その場合、磁化力は次のようになります。各線の磁化力の合計。
レンツの法則 — 電磁誘導のすべてのケースをカバーし、発生する EMF の方向を決定できるようにする基本規則。誘導。
レンツの法則によれば、この方向はすべての場合において、出現する起電力によって生成される電流が起電力の出現を引き起こした変化を防ぐようなものです。誘導。この法律は定性的な定式化です エネルギー保存の法則 電磁誘導に応用されています。
電磁誘導の法則、ファラデーの法則 — 磁気現象と電気現象の間の関係を確立する法則。回路内の電磁誘導の EMF は、この回路によって境界付けられる表面を通る磁束の変化率と数値的に等しく、符号が逆です。 EMF 場の大きさは磁束の変化率に依存します。
ファラデーの法則 (イギリスの物理学者 M. ファラデー (1791-1867) にちなんで命名) — 電気分解の基本法則。
導電性溶液 (電解質) を通過する電気の量と電極上に放出される物質の量の間には関係があります。
直流電流 I が 1 秒あたり電解液を通過すると、q = It、m = kIt となります。
ファラデーの第 2 法則: 元素の電気化学当量は、その化学当量に直接比例します。
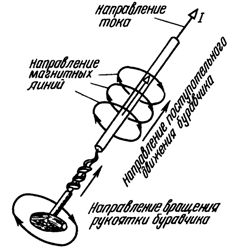
ドリルルール — 磁場の方向を決定できるルール。 電流の方向… ジンバルの前方への動きと電流の流れが一致すると、ハンドルの回転方向が磁力線の方向を示します。あるいは、グリップハンドルの回転方向がループ内の電流の方向と一致する場合、ジンバルの並進運動は、ループで囲まれた表面を貫通する磁力線の方向を示します。
ギムレットルール
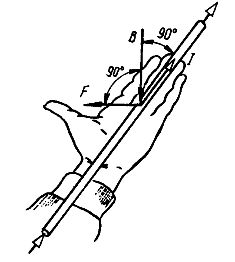
左手の法則 — 電磁力の方向を決定できる規則。磁気誘導のベクトルが入るように左手の手のひらを配置すると（伸ばした4本の指が電流の方向と一致します）、直角に曲がった左手の親指は電流の方向を示します。電磁力。
左手の法則
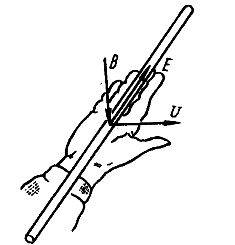
右手の法則 — 電磁誘導の誘導起電力の方向を決定できる規則。右手の手のひらは磁力線が入る位置に置きます。直角に曲がった親指はドライバーの進行方向と一致します。伸ばした 4 本の指は、誘導起電力の方向を示します。
右手の法則