電気回路の時定数 — それが何であり、どこで使用されるか

周期的なプロセスは自然界に固有のものです。昼の後に夜が来る、暖かい季節が寒くなるなどです。これらの出来事の周期はほぼ一定であるため、厳密に決定できます。さらに、例として挙げた周期的な自然現象は、少なくとも人の寿命の観点からは減価しないと主張する権利がある。

しかし、テクノロジー、特に電気工学やエレクトロニクスの分野では、すべてのプロセスが周期的かつ連続的であるわけではありません。通常、一部の電磁プロセスは最初に増加し、その後減少します。多くの場合、物質は振動の開始段階にのみ限定されており、実際に速度を上げる時間がありません。

電気工学では、いわゆる指数関数的過渡現象がよく見られます。その本質は、システムがある平衡状態に到達しようとしているだけで、最終的には静止状態に見えるということです。このような推移は増加または減少のいずれかになります。

外力は最初に動的システムの平衡を解除し、その後このシステムが元の状態に自然に戻ることを妨げません。この最後の段階は、いわゆる移行プロセスであり、一定の期間が特徴です。さらに、システムのバランスを崩すプロセスも、特有の持続時間を伴う一時的なプロセスです。

いずれにせよ、過渡プロセスの時定数は時間特性と呼ばれ、このプロセスの特定のパラメータが変化するまでの時間を決定します «e»、つまり約 2.718 倍増加または減少します初期状態との比較。

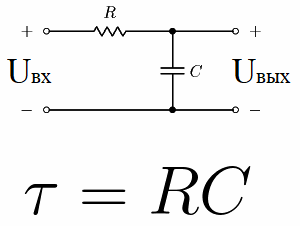
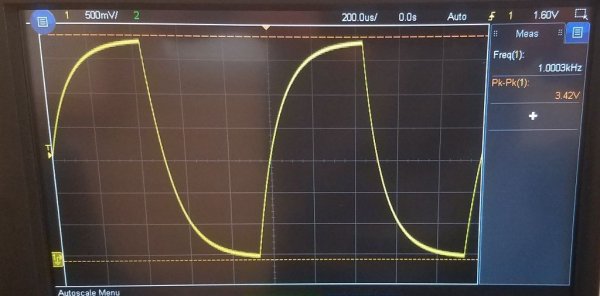
たとえば、DC 電圧源、コンデンサ、抵抗器で構成される電気回路を考えてみましょう。このようにコンデンサと抵抗を直列に接続した回路をRC積分回路と呼びます。

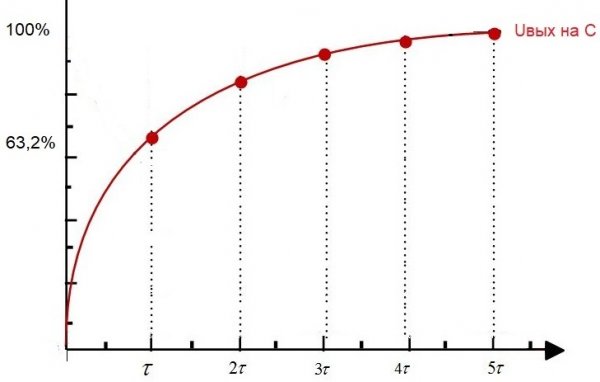
このような回路に電力を供給する最初の瞬間、つまり入力に定電圧 Uin を設定すると、Uout (コンデンサ内の電圧) は指数関数的に増加し始めます。

時間 t1 の後、コンデンサ電圧は入力電圧の 63.2% に達します。したがって、最初の瞬間から t1 までの時間間隔が、この RC 回路の時定数になります。

この鎖定数は«タウ»と呼ばれ、秒単位で測定され、対応するギリシャ文字で示されます。数値的には、RC 回路の場合、これは R * C に等しくなります。R の単位はオーム、C の単位はファラッドです。

集積化 RC 回路は、高い周波数を遮断 (抑制) し、低い周波数を通過させる必要がある場合に、電子機器でローパス フィルターとして使用されます。

実際には、このような濾過のメカニズムは次の原理に基づいています。交流の場合、コンデンサは容量性抵抗として機能し、その値は周波数に反比例します。つまり、周波数が高くなるほどコンデンサのリアクタンス（オーム単位）は低くなります。

したがって、RC 回路に交流電流が流れると、分圧器のアームと同様に、流れる電流の周波数での静電容量に比例して、コンデンサの両端で一定の電圧が降下します。

入力交流信号のカットオフ周波数と振幅がわかっている場合、設計者が RC 回路内でそのようなコンデンサと抵抗を選択することは難しくありません。リアクタンスが抵抗とともに分圧器に入力されるため、カットオフ周波数 (周波数の上限) がコンデンサに影響します。

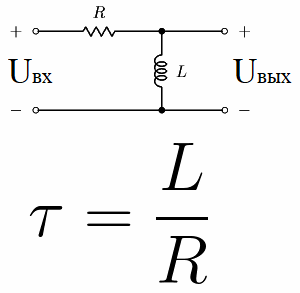
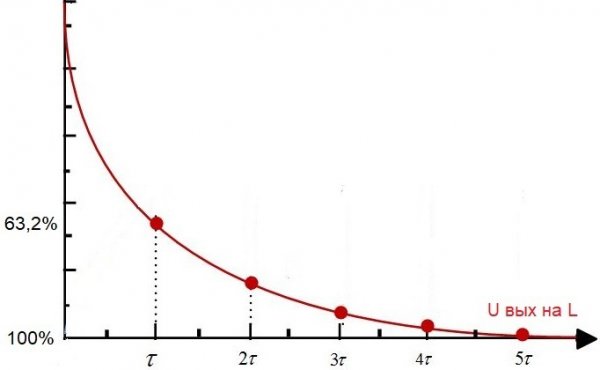
ここで、いわゆる微分回路を考えてみましょう。抵抗とインダクタを直列に接続した回路、RL回路です。その時定数は数値的には L / R に等しくなります。ここで、L はヘンリー単位のコイルのインダクタンス、R はオーム単位の抵抗器の抵抗です。

電源からの定電圧がこのような回路に印加されると、しばらくして tau が経過すると、コイルの電圧は U in に比べて 63.2% 減少します。これは、この電気回路の時定数の値に完全に一致します。 。

AC 回路 (交流信号) では、低周波数をカットオフ (抑制) する必要があり、それより上の周波数 (カットオフ周波数を超える、つまり周波数の下限) が省略される場合、LR 回路がハイパス フィルターとして使用されます。したがって、コイルのインダクタンスが大きいほど、周波数は高くなります。

上で説明した RC 回路の場合と同様に、ここでも分圧器の原理が使用されます。 RL 回路を通過する高周波電流は、抵抗とともに分圧器の一部である誘導抵抗と同様に、インダクタンス L での電圧降下が大きくなります。設計者の仕事は、コイルの最小 (境界) 電圧が正確に境界周波数で得られるように、そのような R と L を選択することです。