電気力学の最も重要な法則を簡潔でわかりやすい形式で解説
現代世界における電気力学の重要性は、主に、長距離電線を介した電気エネルギーの伝送、配電方法、および電気の他の形式への変換に関して、電気力学が切り開く幅広い技術的可能性に関連しています。 機械的、熱的、光など。
発電所で生成された電気エネルギーは、何マイルにもわたる送電線を介して家庭や産業施設に送られ、そこで電磁力によってさまざまな機器、家庭用電化製品、照明、暖房装置などのモーターが駆動されます。一言で言えば、現代経済を想像することは不可能であり、壁にコンセントのない部屋などありえないのです。
これらすべては、理論を電気の実際の応用に結び付けることを可能にする電気力学の法則の知識のおかげでのみ可能になりました。この記事では、これらの法則のうち最も実用的な 4 つを詳しく見ていきます。
電磁誘導の法則
電磁誘導の法則は、発電所に設置されたすべての発電機の動作の基礎です。しかしすべては、1831 年にコイルに対する電磁石の動きの実験でマイケル・ファラデーによって発見された、ほとんど目に見えない電流から始まりました。
ファラデーは発見の見通しについて尋ねられたとき、実験の結果をまだ成長していない子供の誕生に例えました。すぐに、この新生児は文明世界全体の様相を変えた真の英雄になりました。参照 — 電磁誘導の法則の実用化
ドイツの歴史ある水力発電所の発電機
現代の発電所の発電機 単なる磁石の付いたコイルではありません。それは、鋼構造物、絶縁された銅バスバーの多数のコイル、大量の鉄、絶縁材、さらにはミリメートルの何分の一の精度で製造された多数の小さな部品を含む巨大な構造物です。
もちろん、自然界ではそのような複雑な装置は見つかりませんが、実験という自然は、利用可能な外力の影響下で機械的な動きによって装置がどのように機能して電気を生成するかを人間に示しました。
発電所で生成された電気は変換され、配電され、再び変換されます。 電源変圧器、その仕事も電磁誘導現象に基づいていますが、変圧器のみが発電機とは異なり、その設計に常に動く部品が含まれておらず、代わりにコイルを備えた磁気回路が含まれています。
交流巻線(一次巻線)は磁気回路に作用し、磁気回路は二次巻線(トランスの二次巻線)に作用します。変圧器の二次巻線からの電気は現在、消費者に配電されています。これらすべては、電磁誘導現象と、ファラデーという名前が付けられた対応する電気力学の法則の知識のおかげで機能します。
電磁誘導の法則の物理的意味は、磁場が時間の経過とともに変化するときの渦電場の出現であり、これはまさに動作中の変圧器で起こります。
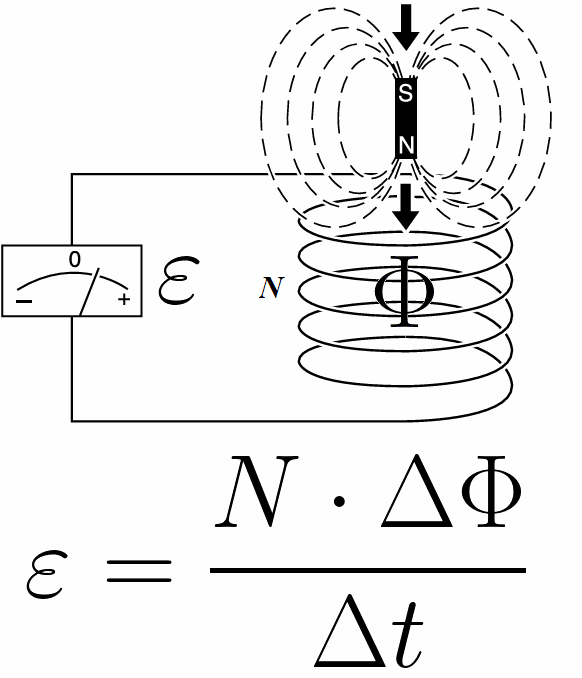
実際には、導体によって境界が定められた表面を貫く磁束が変化すると、導体内に EMF が誘導され、その値は磁束の変化率 (F) に等しくなりますが、誘導された EMF の符号はは、行われた変更の割合 F と逆になります。この関係は、「フロー ルール」とも呼ばれます。
ループを貫く磁束を直接変更することに加えて、ループ内で EMF を取得する別の方法も可能です。 ローレンツ力を利用して.
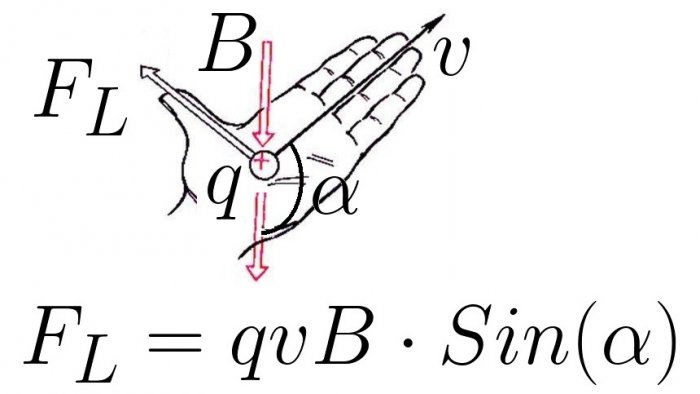
ご存知のとおり、ローレンツ力の大きさは、磁場内の電荷の移動速度、磁場の誘導の大きさ、誘導ベクトルに対して特定の電荷が移動する角度に依存します。磁場の:
正電荷に対するローレンツ力の方向は、「左手」の法則によって決まります。つまり、磁気誘導のベクトルが手のひらに入るように左手を置き、伸ばした 4 本の指を手のひらの移動方向に置くと、正電荷の場合、親指を 90 度に曲げると、ローレンツ力の方向が示されます。
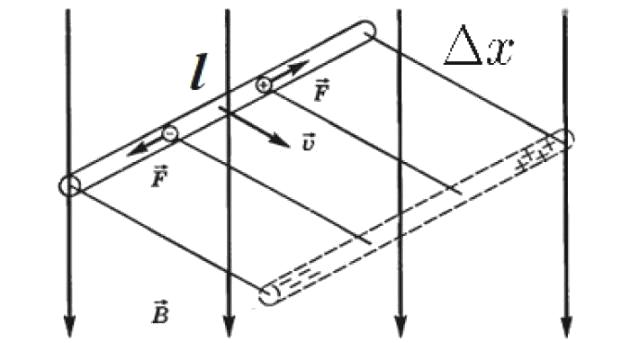
このような場合の最も単純な例を図に示します。ここで、ローレンツ力により、磁場中を移動する導体 (銅線など) の上端は正に帯電し、下端は負に帯電します。これは、電子が負の電荷を持っており、ここを移動するのは電子であるためです。 。
電子は、電子とワイヤの反対側の正電荷との間のクーロン引力がローレンツ力と釣り合うまで下に移動します。
このプロセスにより、導体に誘導の EMF が発生しますが、これは電磁誘導の法則に直接関係していることが判明しました。実際、ワイヤ内の電界強度 E は次のように求めることができます (ワイヤがベクトル B に対して直角に移動すると仮定します)。
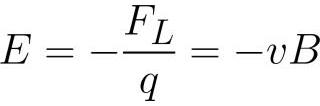
したがって、誘導のEMFは次のように表すことができます。
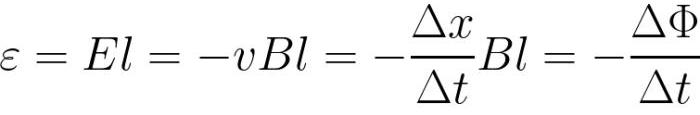
与えられた例では、磁束 F 自体 (物体として) は空間内で変化しませんが、ワイヤーは磁束が存在する領域を横切り、ワイヤーが横切る領域を簡単に計算できることに注意してください。所定の時間内に空間のその領域を移動することによって (つまり、前述の磁束の変化率)、
一般的なケースでは、«磁束則» によれば、回路内の EMF は、その値が大きいかどうかに関係なく、その回路を通る磁束の変化率を反対の符号でとったものに等しいと結論付ける権利があります。磁束 F は、ループの変位 (磁束を横切る) または変形、またはその両方の結果として、固定ループでの時間の経過に伴う磁場の誘導の変化により直接変化します。
アンペールの法則
発電所で生成されたエネルギーの大部分は企業に送られ、そこでさまざまな金属切断機のエンジンに電力が供給されます。電気モーターの動作は設計者の理解に基づいています。 アンペールの法則.
この法則は、1820 年にアンドレ マリー アンペールによって直流に関して作成されました (この法則が電流相互作用の法則とも呼ばれるのは偶然ではありません)。
アンペールの法則によれば、同じ方向の電流が流れる平行なワイヤは互いに引き付けられ、反対方向の電流が流れる平行なワイヤは互いに反発します。さらに、アンペールの法則は、特定の磁場で電流が流れる導体に磁場が作用する力を決定するための経験則を指します。
アンペールの法則は、簡単に次のように言えます。磁場内で電流が流れる導体の要素に磁場が作用する力 (アンペール力と呼ばれます) は、導体内の電流量に正比例します。と、磁気誘導の値からのワイヤの長さの要素のベクトル積。
したがって、アンペール力の係数を求める式には、磁気誘導ベクトルとこの力が作用する導体の電流ベクトルの間の角度の正弦が含まれます (アンペール力の方向を決定するには、左手の法則を使用できます) ):
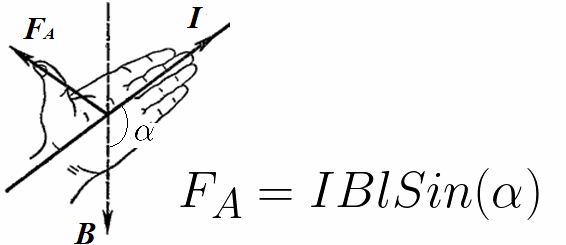
アンペールの力は、相互作用する 2 つの導体に適用されると、それらの導体のそれぞれの電流の方向に応じた方向にそれぞれの導体に作用します。
真空中に電流 I1 と I2 が流れる無限に長い 2 本の細い導体があり、どこの導体間の距離も r に等しいと仮定します。ワイヤの単位長さ (たとえば、1 番目のワイヤの 2 番目のワイヤの側) に作用するアンペア力を見つける必要があります。
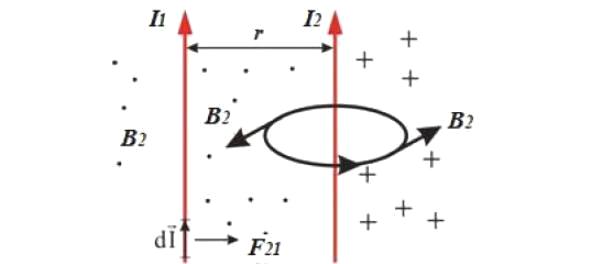
ビオ・サバール・ラプラスの法則によると、電流 I2 が流れる無限導体から距離 r のところで、磁場には次のような誘導が生じます。
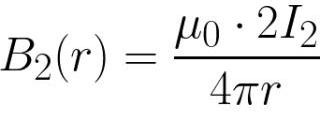
これで、磁場の特定の点 (特定の誘導のある場所) にある最初のワイヤに作用するアンペア力を見つけることができます。
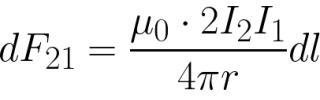
この式を長さにわたって積分し、長さに 1 を代入すると、1 番目のワイヤの 2 番目のワイヤ側の単位長さあたりに作用するアンペア力が得られます。同様の力が、反対方向にのみ、最初のワイヤの側から 2 番目のワイヤに作用します。
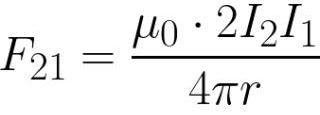
アンペールの法則を理解していなければ、少なくとも 1 つの通常の電気モーターを定性的に設計して組み立てることは不可能です。
ジュール・レンツの法則
すべての電気エネルギー 伝送線路、これらのワイヤが加熱されます。さらに、さまざまな加熱装置に電力を供給したり、タングステン フィラメントを高温に加熱したりするために、大量の電気エネルギーが意図どおりに使用されます。電流の加熱効果の計算は、1841 年に James Joule によって発見され、1842 年に Emil Lenz によって独立して発見されたジュール・レンツの法則に基づいています。
この法則は、電流の熱効果を定量化します。「媒体に直流電流を流したときに媒体の単位体積(w)あたりに発生する熱量は、電流密度(j)と電界強度の値の積に比例する」と定式化されます。 (E)«。
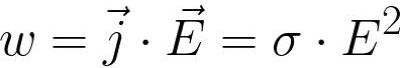
細いワイヤの場合、法則の積分形式が使用されます。「回路のセクションから単位時間あたりに放出される熱の量は、考慮されているセクションの電流の 2 乗とセクションの抵抗の積に比例します。 » 以下のような形式で書かれています。
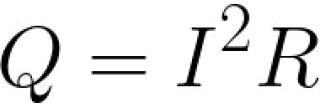
ジュール・レンツの法則は、長距離電線を介した電気エネルギーの伝送において特に実用的に重要です。
結論としては、電力線への電流の熱影響はエネルギー損失につながるため、望ましくないということになります。また、伝達電力は電圧と電流の大きさの両方に線形に依存しますが、加熱電力は電流の二乗に比例するため、電気が伝達される電圧を上げ、それに応じて電流を減らすことが有利です。
オームの法則
電気回路の基本法則 — オームの法則 1826 年にゲオルグ・オームによって発見されました。… 法則は、電線の電気抵抗または導電率(電気伝導度)に応じて、電圧と電流の関係を決定します。現代の用語では、完全な回路に対するオームの法則は次のように記述されます。
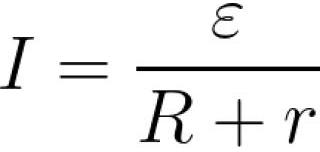
r — 電源内部抵抗、R — 負荷抵抗、e — 電源EMF、I — 回路電流
この記録から、電源から与えられた電流が流れる閉回路内の EMF は次と等しいことがわかります。
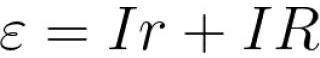
これは、閉回路の場合、電源起電力は外部回路の電圧降下と電源の内部抵抗の合計に等しいことを意味します。
オームの法則は次のように定式化されます。「回路のあるセクションの電流は、その両端の電圧に正比例し、回路のこのセクションの電気抵抗に反比例します。」オームの法則の別の表記法は、コンダクタンス G (電気伝導率) です。
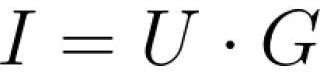
電圧、電流、抵抗とは何ですか、また実際にどのように使用されますか