起磁力、ホプキンソンの法則とは

19世紀後半、英国の物理学者ジョン・ホプキンソンとその弟エドワード・ホプキンソンは、磁気回路の一般理論を開発し、オームの法則（使用法）の類似物である「ホプキンソンの公式」またはホプキンソンの法則と呼ばれる数式を導き出しました。電気回路の計算に使用します)。

したがって、オームの古典法則が電流と起電力 (EMF) の関係を数学的に説明する場合、ホプキンソンの法則は同様に磁束といわゆる 起磁力（MDF）.

その結果、次のことが判明しました。 起磁力は、磁束を生成する電流の能力を特徴付ける物理量です。 そして、磁気回路の MDF は電気回路の EMF に似ているため、この点に関するホプキンソンの法則は磁気回路の計算にうまく使用できます。ホプキンソンの法則の発見日は 1886 年と考えられています。

起磁力 (MDF) の大きさは最初はアンペアで測定されますが、電流または電磁石を備えたコイルについて話している場合は、計算の便宜上、その式をアンペア ターンで使用します。

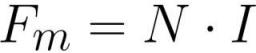
ここで、Fm はコイルの起磁力 [アンペア * ターン]、N はコイルの巻き数 [ターン]、I はコイルの各巻きの電流量 [アンペア]です。

ここに磁束の値を入力すると、磁気回路のホプキンソンの法則は次の形式になります。

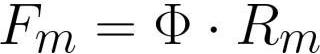
ここで、Fm はコイル内の起磁力 [アンペア * ターン]、F は磁束 [ウェーバー] または [ヘンリー * アンペア]、Rm は磁束導体の磁気抵抗 [アンペア * ターン / ウェーバー] または [ターン/ヘンリー]。

ホプキンソンの法則の原文の定式化は、もともと次のとおりでした。「非分岐磁気回路では、磁束は起磁力に正比例し、総磁気抵抗に反比例する。」つまり、次の法則は、回路内の起磁力、磁気抵抗、磁束の関係を決定します。

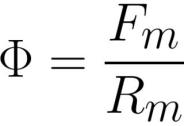
ここで、F は磁束 [ウェーバー] または [ヘンリー * アンペア]、Fm はコイル内の起磁力 [アンペア * 回転数]、Rm は磁束導体の磁気抵抗 [アンペア * 回転数 / ウェーバー] または [ターン/ヘンリー]。

ここで、実際、起磁力 (MDF) は起電力 (EMF) とは根本的な違いがあることに注意することが重要です。起電力 (EMF) は、粒子が磁束の中を直接移動しないのに対し、電流は磁束の作用で発生するという事実にあります。 EMF は、金属ワイヤ内の電子などの荷電粒子の動きを利用します。しかし、MDS のアイデアは、磁気回路の計算の問題を解決するのに役立ちます。

たとえば、その長さ全体にわたって同じ断面積 S のヨークを含む分岐していない磁気回路を考えてみましょう。ヨークの材料は透磁率μを持っています。

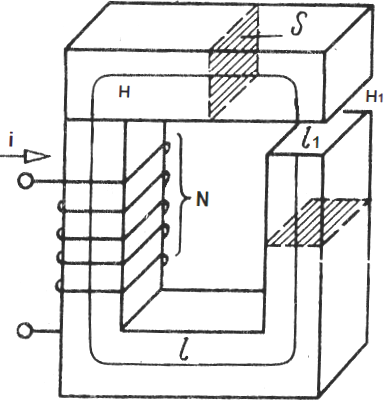
ヨークの隙間 - 異素材、 透磁率 どのミュー1。ヨーク上に配置されたコイルには N 個の巻線が含まれており、コイルの各巻線には電流 i が流れます。磁場循環定理をヨークの中心線に適用します。

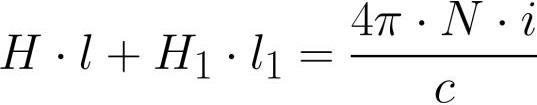
ここで、H はヨーク内部の磁界強度、H1 はギャップ内部の磁界強度、l はヨーク誘導の中心線の長さ (ギャップなし)、l1 はギャップの長さです。

ヨーク内部とギャップ内部の磁束は同じ値を持つため（磁気誘導線の連続性により）、Ф = BS と В = mu * H を書いた後、磁界の強さをさらに詳しく書きます。これを上記の式に代入すると、次のようになります。

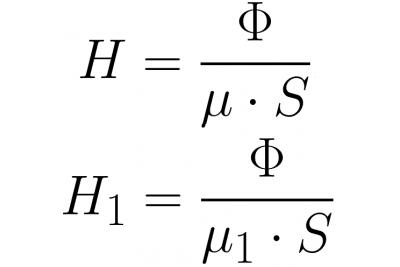
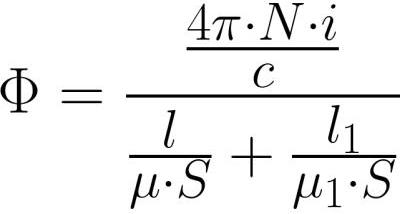
電気回路のオームの法則における EMF のように、MDS が

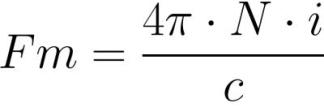
ここで起電力と磁気抵抗の役割を果たします

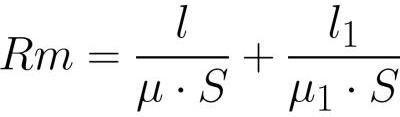
抵抗の役割（類推による） 古典的なオームの法則を使って).