交流回路の力率を間接的に求める原理と方法

力率またはコサインファイは、正弦波交流のユーザーに関して、ネットワークからこのユーザーに供給される総電力 S に対する有効電力消費量 P の比率です。

トータルパワーS一般的な場合、考慮されている回路の電流 I と電圧 U の実効値 (二乗平均平方根) と、ユーザーが不可逆的に消費する有効電力 P の積として定義できます。仕事の操作。

無効電力Qただし、総電力の一部ではありますが、仕事を実行するために消費されるのではなく、ユーザーの回路の一部の要素で交流電界と磁界の生成にのみ関与します。

を除外する 力率の直接測定 電気力学的デバイスの使用 — 位相計、正弦波交流回路のユーザーを特徴付けるこの非常に重要な電気量の値を数学的に正確に理解できるようにする、非常に論理的な間接的な方法があります。

データを見てみましょう 間接的な方法 詳細に、 間接力率測定の原理を理解しましょう。

電圧計、電流計、電力計方式

動電型電力計 可動コイルの回路にアクティブ抵抗が追加された場合は、AC 回路 P で消費される非常にアクティブな電力の値を示します。

ここで、電圧計と電流計を使用して、調査対象の負荷の回路に作用する電流Iと電圧Uの平均値を測定すると、これら2つのパラメータを乗算することで、合計電力Sのみが得られます。 。

次に、特定の負荷の力率 (コサイン ファイ) は、次の式を使用して簡単に求めることができます。

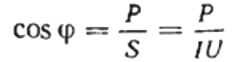
ここで、必要に応じて、無効電力 Q の値、回路の合計抵抗 z を見つけることもできます。 オームの法則、単純に抵抗三角形を作成または表現し、ピタゴラスの定理を使用することで、能動抵抗と反応抵抗だけでなく、

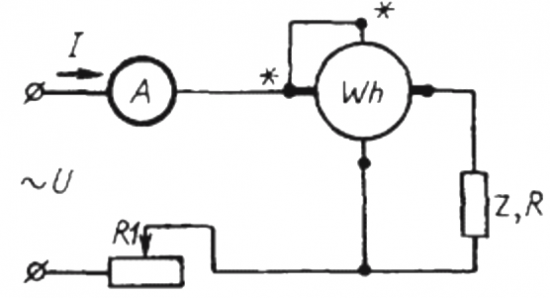
カウンタと電流計方式

この方法を使用するには、最も単純な回路を負荷 Z と電流計に直列に接続する回路を組み立てる必要があります。 電力計 うーん。

1 分程度の一定時間 t の間、ディスクの回転数 N を計算する必要があります。これは、一定時間内に費やされるアクティブ エネルギーの量を示します (つまり、力率）。

ここで、ディスクの回転数 N、係数 k は 1 回転あたりのエネルギー量、I と U はそれぞれ rms 電流と電圧、t は回転をカウントする時間、cosine phi は力率です。

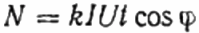
次に、研究対象のユーザー Z の代わりに、同じカウンタを介して、ただし直接ではなく加減抵抗器 R1 を介して、能動負荷 R が回路に含まれます (ユーザー Z の場合、最初のケースと同じ電流 I が得られます)。ディスクＮ１の回転数は同じ時間ｔ維持される。ただし、ここでは負荷がアクティブであるため、コサイン ファイ (力率) は確実に 1 に等しくなります。 したがって、次のようになります。

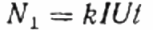
次に、ディスク カウンタの回転比が 1 番目と 2 番目のケースで同じ期間記録されます。これはコサイン ファイ、つまり最初の負荷の力率 (同じ負荷を持つ純粋にアクティブな負荷と比較したもの) になります。現在）：

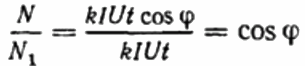
3電流計方式

3 つの電流計を使用して正弦波電流回路の力率を決定するには、まず次の回路を組み立てる必要があります。

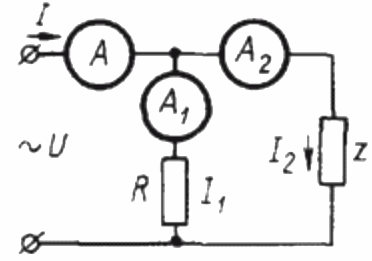
ここで、Z は力率を求める負荷、R は純粋な能動負荷です。

負荷 R は純粋にアクティブであるため、電流 I1 はどの時点でもこの負荷に印加される交流電圧 U と同相であり、この場合、電流 I は電流 I1 と I2 の幾何学和に等しくなります。次に、この位置に基づいて電流のベクトル図を作成します。

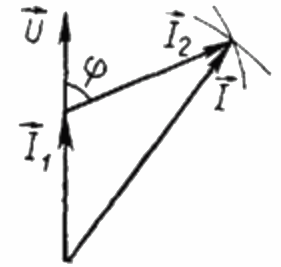
電流のベクトル図では、電流 I1 と電流 I2 の間の鋭角が角度 phi であり、その余弦 (実際には力率の値) は特別な値の表から見つけることができます。三角関数または次の式で計算されます。

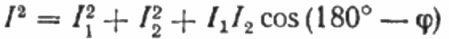
ここから、コサイン ファイ、つまり望ましい力率を表すことができます。

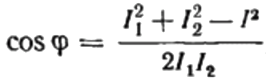
検出された力率の符号 («+» または «-«) は、負荷の性質を示します。力率 (コサインファイ) が負の場合、負荷は本質的に容量性です。力率が正の値の場合、負荷の性質は誘導性です。