基本的な電気量: 電荷、電圧、電流、電力、抵抗
基本的な電気量: 電流、電圧、抵抗、電力。
充電
電気回路における最も重要な物理現象は動きです 電荷… 自然界には、正と負の 2 種類の電荷があります。電荷が引き合うように、電荷が反発するように。これは、正の電荷と負の電荷を同じ量でグループ化する傾向があるという事実につながります。
原子は、負に帯電した電子の雲に囲まれた正に帯電した原子核で構成されています。絶対値での負電荷の合計は原子核の正電荷に等しい。したがって、原子の総電荷はゼロであり、電気的に中性であるとも言えます。
保持できる素材で 電気、一部の電子は原子から分離され、導電性材料内を移動する能力を持っています。これらの電子は移動電荷または電荷キャリアと呼ばれます。
初期状態では各原子は中性であるため、マイナスの電気を帯びた電子が離れると、プラスの電気を帯びたイオンになります。正イオンは自由に移動できず、静止した固定電荷の系を形成します (—を参照) どのような物質が電気を通すのか).
半導体では重要な種類の材料を構成する可動電子は 2 つの方法で移動できます。もう 1 つは、電子が単に負に帯電したキャリアとして動作することです。あるいは、多くの電子の複雑な集合体は、あたかも材料内に正に帯電した移動キャリアがあるかのように移動します。固定料金はどちらの文字でも可能です。
導電性材料は、移動電荷キャリア (2 つの符号のいずれかを持ちます) と反対極性の固定電荷を含む材料と考えることができます。
電気を通さない絶縁体と呼ばれる物質もあります。絶縁体の電荷はすべて固定されています。絶縁体の例としては、空気、雲母、ガラス、多くの金属の表面に形成される酸化物の薄い層、そしてもちろん真空(まったく電荷が存在しない)などがあります。
電荷はクーロン (C) 単位で測定され、通常は Q で表されます。
電子あたりの電荷量または負の電気の量は、数多くの実験を通じて確立されており、1.601 × 10-19 CL または 4.803 × 10-10 の静電荷であることが判明しています。
比較的低い電流でもワイヤを流れる電子の数については、次のようにして考えることができます。電子の電荷は 1.601 · 10-19 CL であるため、クーロンに等しい電荷を生成する電子の数は所定の逆数、つまり 6 · 1018 にほぼ等しくなります。
1 A の電流は 1 秒あたり 1 C の流れに相当し、ワイヤの断面を流れるわずか 1 μmka (10 ~ 12 A) の電流で、1 秒あたり約 600 万個の電子が流れます。このような大きさの電流は同時に非常に小さいため、その検出と測定には実験における重大な困難が伴います。
正イオンの電荷は電子の電荷の整数倍ですが、符号が反対です。単一イオン化された粒子の場合、電荷は電子の電荷と等しいことがわかります。
原子核の密度は電子の密度よりもはるかに高く、原子全体が占める体積のほとんどは空です。
電気現象の概念
2 つの異なる物体をこすり合わせたり、誘導によって、物体に特別な特性、つまり電気を与えることができます。このような物体は帯電していると呼ばれます。
帯電した物体の相互作用に関連する現象は次のように呼ばれます。 電気現象.
帯電した物体間の相互作用は、いわゆる電気力は、運動の速度に関係なく、帯電した物体を反発させたり引き付けたりするという点で、別の性質の力とは異なります。
このように、帯電した物体間の相互作用は、例えば、物体の引力だけを特徴とする重力の相互作用や、電荷の移動の相対速度に依存する磁気起源の力とは異なり、磁気を引き起こします。現象。
電気工学は主に特性の外部発現の法則を研究します 帯電した体 — 電磁場の法則。
電圧
反対の電荷間の強い引力のため、ほとんどの材料は電気的に中性です。プラスとマイナスの電荷を分離するにはエネルギーが必要です。
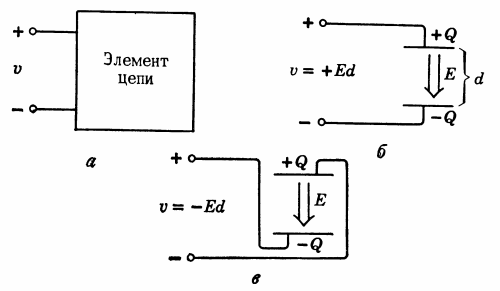
図では。図1は、距離dだけ離間した、最初は帯電していない2つの導電性プレートを示す。板の間の空間は空気などの絶縁体で満たされているか、真空になっていると仮定します。
米。 1. 2 つの導電性の、最初は帯電していないプレート: a — プレートは電気的に中性です。 b — 電荷 -Q が底部プレートに転送されます (プレート間に電位差と電場が存在します)。
図では。図 1 では、両方のプレートは中性であり、上部プレートの合計ゼロ電荷は、電荷 +Q と -Q の合計で表すことができます。図では。図1bに示すように、電荷−Qは上部プレートから下部プレートに転送される。図の場合。 1bでは、プレートをワイヤで接続します。すると、反対の電荷の引力によって電荷がすぐに元に戻り、図1に示す状況に戻ります。 1、a.正電荷は負に帯電したプレートに移動し、負電荷は正に帯電したプレートに移動します。
図に示す帯電したプレートの間のことを言います。図1bに示すように、電位差があり、正に帯電した上部プレートの電位は、負に帯電した下部プレートよりも高い。一般に、2 点間の導通により電荷の移動が生じる場合、2 点間に電位差が生じます。
正電荷は高電位点から低電位点へ移動しますが、負電荷の移動方向は逆で、低電位点から高電位点へ移動します。
電位差を測定する単位はボルト (V) です。電位差は電圧と呼ばれ、通常は文字 U で表されます。
2 点間の張力を定量化するには、次の概念が使用されます。 電界…図の場合。図1bに示すように、プレート間には、より高い電位の領域(正極板から)からより低い電位の領域(負極板へ)に向かう均一な電場が存在する。
この場の強さは、1 メートルあたりのボルトで表され、プレート上の電荷に比例し、電荷の分布がわかっていれば物理法則から計算できます。電場の大きさとプレート間の電圧 U の関係は、U = E NS e (ボルト = ボルト / メートル x メートル) の形式になります。
したがって、低い電位から高い電位への遷移は、場の方向に逆らう動きに相当します。より複雑な構造では、電場はどこでも均一ではない可能性があり、2 点間の電位差を決定するには、方程式 U = E NS e を繰り返し使用する必要があります。
関心のあるポイント間の間隔は多くのセクションに分割されており、各セクションはフィールドがその中で均一になるのに十分な大きさです。次に、方程式が各セグメント U = E NS e に連続的に適用され、各セクションの電位差が合計されます。したがって、電荷と電場の分布がどのような場合でも、任意の 2 点間の電位差を見つけることができます。
電位差を求める際には、2点間の電圧の大きさだけでなく、どちらの点の電位が最も高いかを示す必要があります。ただし、複数の異なる要素を含む電気回路では、どの点が最も高い電位を持つかを事前に判断できるとは限りません。混乱を避けるために、記号の条件を受け入れる必要があります (図 2)。
米。 2… 電圧の極性を決定します (電圧は正または負にすることができます)。
バイポーラ回路要素は、2 つの端子を備えたボックスで表されます (図 2、a)。ボックスから端子につながる線は、理想的な電流導体であると想定されます。一方の端子にはプラス記号が付けられ、もう一方の端子にはマイナス記号が付いています。これらの文字は相対極性を固定します。図の電圧U。 2 であり、U = (端子«+»の電位) — (端子«-«の電位)という条件によって決定されます。
図では。図2bでは、帯電したプレートが端子に接続され、「+」端子がより高い電位のプレートに接続される。ここで、電圧 U は正の数です。図では。図2では、«+»端子が下部電位プレートに接続されています。その結果、負の電圧が得られます。
応力表現の代数形式について覚えておくことが重要です。極性が決定されると、正の電圧は«+»端子の電位が高いことを意味し、負の電圧は«-»端子の電位が高いことを意味します。
現在
正の電荷キャリアは高電位領域から低電位領域に移動し、負の電荷キャリアは低電位領域から高電位領域に移動することが上で指摘された。料金の送金は期限切れを意味します 電気.
図では。図 3 は、電流の流れのいくつかの単純なケースを示しています。表面は C が選択され、概念的な正の方向が示されています。時間 dt が経過してセクション S を通過すると、総電荷 Q が選択した方向に流れる場合、S を流れる電流 I は I = dV/dT に等しくなります。電流の測定単位はアンペア (A) (1A = 1C / s) です。
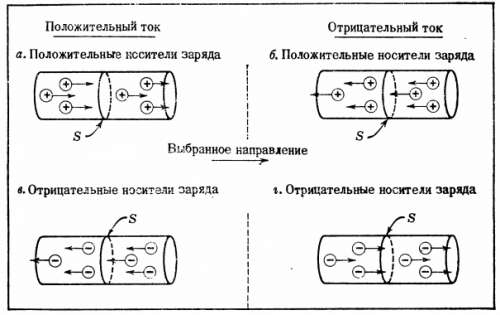
米。 3…電流の方向と携帯料金の流れの方向の関係。表面 C を通る正電荷の流れが選択した方向と一致する場合、電流は正 (a および b) になります。表面を横切る正電荷の流れが選択した方向と反対の場合、電流は負になります (b および d)。
現在の Iz の符号を決定する際に困難が生じることがよくあります。移動電荷キャリアが正の場合、正の電流は選択された方向への移動電荷キャリアの実際の動きを表し、負の電流は選択された方向と反対の移動電荷キャリアの流れを表します。
携帯電話会社がマイナスの場合は、電流の方向を決定するときに注意する必要があります。図を考えてみましょう。 3dでは、負の移動電荷キャリアが選択された方向にSを横切ります。各キャリアが電荷 -q を持ち、S を通過する流量が 1 秒あたり n キャリアであると仮定します。 dt の間、選択された方向への電荷 C の総通過量は dV = -n NS q NS dt となり、これは電流 I = dV/ dT に相当します。
したがって、図 3d の電流は負になります。さらに、この電流は、電荷 + q を持つ正のキャリアが表面 S を選択した方向とは反対の方向に毎秒 n キャリアの速度で移動することによって生成される電流と一致します(図 3、b)。したがって、2 桁の電荷は 2 桁の電流に反映されます。電子回路のほとんどの場合、電流の符号は重要であり、どの電荷キャリア (正または負) がその電流を運ぶかは問題ではありません。したがって、多くの場合、電流について話すとき、彼らは電荷キャリアが正であると仮定します (—を参照) 電流の方向).
しかし、半導体デバイスでは、正と負の電荷キャリアの違いがデバイスの動作にとって重要です。これらのデバイスの動作を詳細に検査すると、携帯電話の充電キャリアの兆候が明確に区別されるはずです。特定の領域を流れる電流の概念は、回路要素を流れる電流に簡単に一般化できます。
図では。図4はバイポーラ素子を示す。正の電流の方向は矢印で示されています。
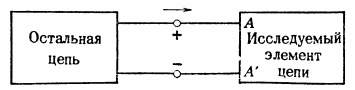
米。 4. 回路要素を流れる電流。電荷は、端子 A を介して速度 i (クーロン/秒) でセルに入り、同じ速度で端子 A' を介してセルから出ます。
回路素子に正の電流が流れると、正の電荷が毎秒 i クーロンの速度で端子 A に入ります。しかし、すでに述べたように、材料 (および回路要素) は通常、電気的に中性のままです。 (図 1 の「充電済み」セルでも、総電荷はゼロです。) したがって、電荷が端子 A を介してセルに流入する場合、同量の電荷が同時に端子 A' を介してセルから流出する必要があります。回路素子を流れる電流の連続性は、素子全体の中性から生じます。
力
回路内のバイポーラ要素は端子間に電圧がかかり、電流が流れる可能性があります。電流と電圧の符号は独立して決定できますが、電圧と電流の極性の間には重要な物理的関係があり、これを明確にするために通常は追加の条件が必要になります。
図では。図 4 は、電圧と電流の相対極性がどのように決定されるかを示しています。電流方向を選択すると《+》端子に電流が流れます。この追加条件が満たされると、重要な電気量、つまり電力を決定できます。図の回路要素を考えてみましょう。 4.
電圧と電流が正の場合、高電位点から低電位点へ正電荷が連続的に流れます。この流れを維持するには、正電荷を負電荷から分離し、それらを«+»端子に導入する必要があります。この継続的な分離には、継続的なエネルギーの消費が必要です。
電荷が要素を通過すると、このエネルギーが放出されます。また、エネルギーは保存する必要があるため、回路素子内で熱として放出されるか (トースターなど)、蓄えられるか (車のバッテリーを充電する場合など) のいずれかになります。このエネルギー変換が起こる速度はと呼ばれます 力 式 P = U NS Az (ワット = ボルト x アンペア) によって決定されます。
電力の測定単位はワット (W) で、これは 1 J のエネルギーを 1 秒に変換することに相当します。図で定義された極性による電圧と電流の積に等しい電力。 4 は代数的な量です。
上記の場合と同様に P > 0 の場合、電力は要素内で散逸または吸収されます。 P < 0 の場合、この場合、要素は接続されている回路に電力を供給します。
抵抗素子
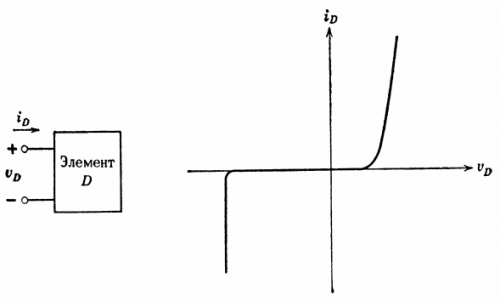
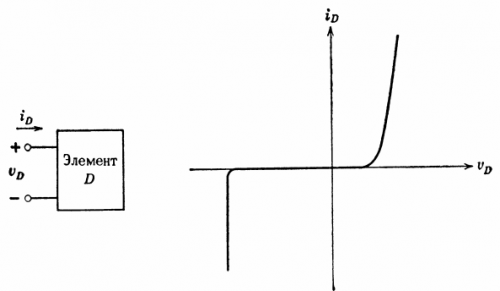
回路要素ごとに、端子電圧と要素を流れる電流の間の特定の関係を記述することができます。抵抗素子は電圧と電流の関係をプロットできる素子で、このグラフを電流電圧特性といいます。このような機能の例を図に示します。 5.
米。 5. 抵抗素子の電流電圧特性
要素 D の端子の電圧がわかっている場合、グラフから要素 D を流れる電流を求めることができます。同様に、電流がわかっていれば、電圧を決定できます。
完璧な抵抗
理想的な抵抗 (または抵抗) は次のとおりです。 線形抵抗素子… 線形性の定義によれば、線形抵抗素子における電圧と電流の関係は、電流が 2 倍になると電圧も 2 倍になるということです。一般に、電圧は電流に比例する必要があります。
電圧と電流の比例関係を次のようにいいます。 回路の一部に関するオームの法則 U = I NS R (R は素子の抵抗) と I = G NS U (G = I / R は素子の導電率) の 2 つの方法で記述されます。抵抗の単位はオーム(ohm)、導電率の単位はジーメンス(cm)です。
理想抵抗の電流電圧特性を図に示します。 6. グラフは、Az/R に等しい傾きを持つ原点を通る直線です。
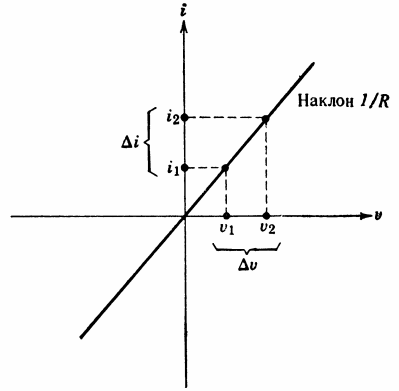
米。 6. 理想抵抗器の名称 (a) と電流電圧特性 (b)。
完璧な抵抗力を備えたパワー
理想的な抵抗によって吸収される電力を表すと、次のようになります。
P = U NS I = I2NS R、P = U2/R
理想的な抵抗で吸収される電力が電流 (または電圧) の 2 乗に依存するのと同じように、理想的な抵抗で吸収される電力 v の符号は R の符号に依存します。ただし、負の抵抗値が使用されることもあります。特定のモードで動作する特定の種類のデバイスをシミュレートする場合、通常、実際の抵抗はすべて正になります。これらの抵抗の場合、吸収される電力は常に正になります。
抵抗によって吸収される電気エネルギー、acc エネルギー保存の法則, 他の種族にNS変身しなければなりません。ほとんどの場合、電気エネルギーはジュール熱と呼ばれる熱エネルギーに変換されます。排泄率 ジュール熱 抵抗という点では、電気エネルギーの吸収率と一致します。例外は抵抗素子 (電球やスピーカーなど) で、吸収されたエネルギーの一部が他の形式 (光や音のエネルギー) に変換されます。
主な電気量の相互関係
直流の場合、基本単位は図に示されています。 7。
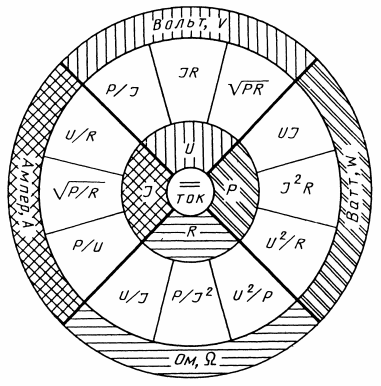
米。 7. 主な電気量の相互関係
電流、電圧、抵抗、電力という 4 つの基本単位は、確実に確立された関係によって相互接続されているため、直接測定だけでなく間接測定を行ったり、他の測定値から必要な値を計算したりすることもできます。したがって、回路の一部の電圧を測定するには電圧計が必要ですが、電圧計がない場合でも、回路内の電流とこの部分の電流抵抗がわかれば、電圧の値を計算できます。