電源とは何ですか?

現代人は日常生活や仕事の中で常に電気に遭遇し、電流を消費する機器や電流を生成する機器を使用しています。彼らと協力するときは、技術的特性に固有の能力を常に考慮する必要があります。

あらゆる電気機器の主な指標の 1 つは、電気エネルギーなどの物理量です。電気の生成、伝達、または他の種類のエネルギー (熱、光、熱など) への変換の強度または速度を呼ぶのが通例です。機械的な。

産業目的での大規模な電気エネルギーの輸送または転送は、次の基準に従って行われます。 高圧送電線.

変身 電気エネルギー 変電所で実施されます。

家庭用および産業用機器ではさまざまな目的で電力消費が発生します。その一般的なタイプの 1 つは、 さまざまな定格の白熱電球.

DC 回路と AC 回路の発電機、送電線、および消費者の電力は同じ物理的意味を持ち、同時に複合信号の形状に応じて異なる比率で表現されます。一般的なパターン、瞬間値の概念を定義するには...電気の変換速度の時間依存性が再び強調されます。

瞬時電力の決定

理論電気工学では、電流、電圧、電力の基本的な関係を導き出すために、ある時点で固定された瞬時値の形でのイメージが使用されます。

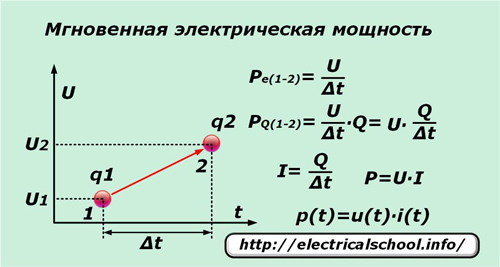
非常に短い時間 Δt の間に、電圧 U の影響下にある単一の素電荷 q が点 «1» から点 «2» に移動すると、これらの点間の電位差に等しい仕事をします。これを時間間隔 Δt で割ると、単位充電あたりの瞬時電力 Pe の式が得られます (1-2)。

印加電圧の作用下で単一の電荷が移動するだけでなく、この力の影響下にあるすべての隣接する電荷も移動するため、その数は便宜的に数値 Q で表され、電力 PQ の瞬時値となります。 (1-2) を書くことができます。

単純な変換を実行した後、電力 P の式と、その瞬時値 p (t) の瞬時電流 i (t) と電圧 u (t) の積の成分への依存性が得られます。

定電力の決定

V 直流回路 回路部分の電圧降下の大きさと回路部分を流れる電流は変化せず安定しており、瞬時値と等しくなります。したがって、この回路の電力は、説明図に示すように、これらの値を掛けるか、完全な作業 A をその実行期間で割ることによって決定できます。

交流電力の決定

電気ネットワークを介して伝送される電流と電圧の正弦波変動の法則は、そのような回路における電力の表現に影響を与えます。ここでは皮相電力が関係します。これは電力の三角形で表され、有効成分と無効成分で構成されます。

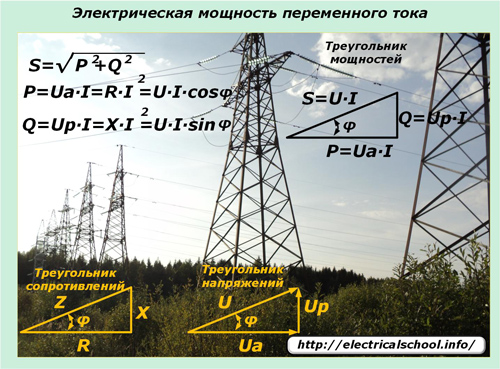
正弦波状の電流は、全区間に異種負荷が混在した電力線を通過しても高調波の形状は変化せず、無効負荷での電圧降下はある方向に位相がシフトします。モーメント値の式は、回路内の電力変化とその方向に対する適用負荷の影響を理解するのに役立ちます。

同時に、発電機から消費者に流れる電流の方向と、作成された回路を介して伝送される電力は完全に異なるものであり、場合によっては一致しないだけでなく、一致しない可能性があるという事実にすぐに注意してください。反対方向に向けられます。

さまざまなタイプの負荷に対する、理想的で純粋な表現としての次の関係を考慮してください。

• アクティブ;

• 容量性;

• 誘導的な。

有効負荷電力損失

発電機が理想的な正弦波電圧 u を生成し、それが回路の純粋にアクティブな抵抗に適用されると仮定します。電流計 A と電圧計 V は、t ごとに電流 I と電圧 U を測定します。

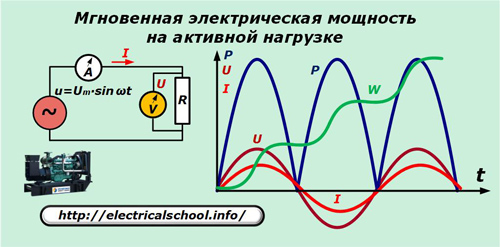
このグラフは、電流の正弦波とアクティブ抵抗の両端の電圧降下が周波数と位相で一致し、同じ振動を起こしていることを示しています。それらの積によって表される力は 2 倍の周波数で振動し、常に正の値を保ちます。

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt)。

表現に行くと 動作電圧とすると、p = P ∙ (1-cos2ωt) が得られます。

次に、1 つの振動 T の期間にわたってパワーを積分すると、この間隔中のエネルギー利得 ΔW が増加することがわかります。グラフに示すように、時間の経過とともに、抵抗は電力の新たな部分を消費し続けます。

無効負荷では、エネルギー消費の特性が異なり、形状も異なります。

容量性電力損失

発電機の電気回路で、抵抗要素を静電容量 C のコンデンサに置き換えます。

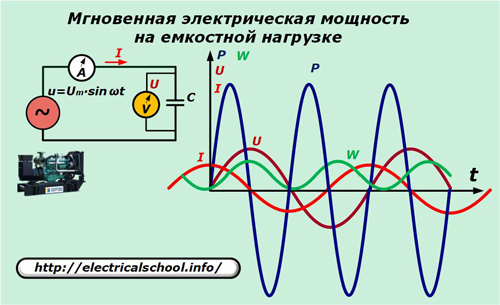
電流と静電容量の電圧降下の関係は、比 I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt で表されます。

電流の瞬時値と電圧を乗算して、容量性負荷によって消費される電力の値を取得します。

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2 ∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt

ここでは、印加電圧の 2 倍の周波数で電力がゼロ付近で変動していることがわかります。高調波周期の合計値とエネルギー利得はゼロです。

これは、エネルギーが回路の閉回路に沿って両方向に移動しますが、仕事をしないことを意味します。このような事実は、電源電圧が絶対値で増加すると、電力は正となり、回路を通るエネルギーの流れがコンテナに向けられ、そこでエネルギーが蓄積されるという事実によって説明されます。

電圧が下降高調波セクションに渡った後、エネルギーはコンデンサから回路を経て電源に戻されます。どちらのプロセスでも有益な作業は行われません。

誘導負荷での電力損失

ここで、電源回路のコンデンサをインダクタンス L に置き換えます。

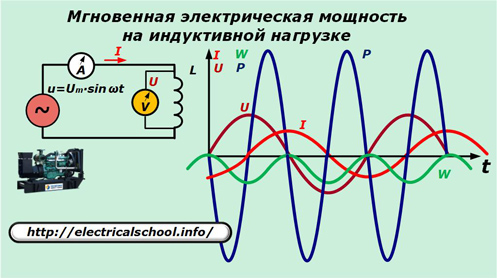
ここで、インダクタンスを流れる電流は次の比率で表されます。

I = 1 / L∫udt = -Um / ωL ∙ cos ωt。

それから、私たちは得ます

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ (2ХL) ∙ sin2ωt

結果として得られる式により、電力の方向の変化の性質とインダクタンスのエネルギーの増加がわかります。インダクタンスは、静電容量と同様に、仕事をするのに役に立たない同じ振動を実行します。

無効負荷で放出される電力は無効成分と呼ばれます。理想的な条件では、接続ワイヤにアクティブな抵抗がない場合、接続ワイヤは無害であるように見え、害を引き起こすことはありません。しかし、実際の電力条件では、周期的な過渡現象や無効電力の変動により、接続線を含むすべてのアクティブ要素が加熱され、そのためにエネルギーが消費され、供給される電源の全電力の値が減少します。

電力の無効成分との主な違いは、無効成分が有益な仕事をまったく実行しないことですが、電気エネルギーの損失と機器への過剰な負荷につながり、危機的な状況では特に危険です。

このような理由から、無効電力の影響を排除するには、特に その補償のための技術システム.

混合負荷時の配電

例として、アクティブな容量特性を持つ発電機の負荷を使用します。

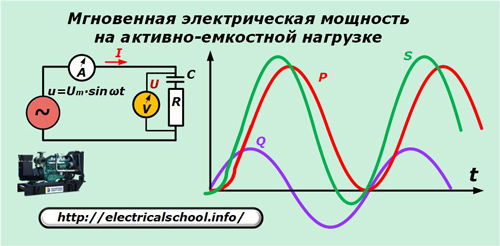
図を簡略化するために、電流と電圧の正弦波は所定のグラフには示されていませんが、負荷の能動容量性の性質により、電流ベクトルが電圧よりも先行することに留意する必要があります。

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ)。

変換後、p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt が得られます。

最後の式のこれら 2 つの項は、瞬時皮相電力の有効成分と無効成分です。これらのうち最初のものだけが有用な機能を果たします。

電力測定ツール

電気の消費量を分析して計算するには、古くから呼ばれる測定装置が使用されます。 「カウンター」… 彼らの仕事は、電流と電圧の実効値を測定し、それらを情報の出力と自動的に乗算することに基づいています。

メーターは、負荷がかかっている状態でメーターのスイッチが入った瞬間から電気製品の動作時間を増分ベースでカウントすることにより、エネルギー消費量を表示します。

AC 回路の電力の有効成分を測定するには、 電力計、およびリアクティブ - 電圧計。それぞれに異なる単位指定があります。

• ワット (W, W);

• var (var、var、var)。

総エネルギー消費量を決定するには、電力計と無効電力計の測定値に基づいて電力三角公式を使用してその値を計算する必要があります。それは独自の単位であるボルトアンペアで表されます。

各単位の受け入れられた指定は、電気技術者がその値だけでなく、電力コンポーネントの性質を判断するのにも役立ちます。