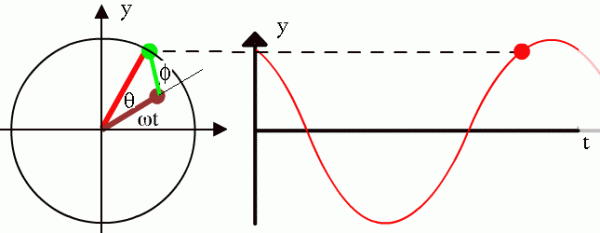
交流の基本パラメータ: 周期、周波数、位相、振幅、高調波振動

交流とは、方向と強さが周期的に変化する電流です。通常、交流の強さは正弦波の法則に従って変化するため、交流は電圧と電流の正弦波状の変動です。

したがって、正弦波電気振動に適用されるものはすべて交流にも適用できます。正弦波振動とは、振動値が正弦の法則に従って変化する振動のことで、今回はACパラメータについて説明します。

EMF の変化と、そのような電源に接続された線形負荷の電流の変化は、正弦波の法則に従います。この場合、交流 EMF、交流電圧、および交流電流は、主な 4 つのパラメータによって特徴付けることができます。

• 期間;

• 周波数;

• 振幅;

• 実効値。

追加のパラメータもあります。

• 角周波数;

• 段階;

• 即時値。

次に、これらすべてのパラメータを個別に、または一緒に見ていきます。

T期

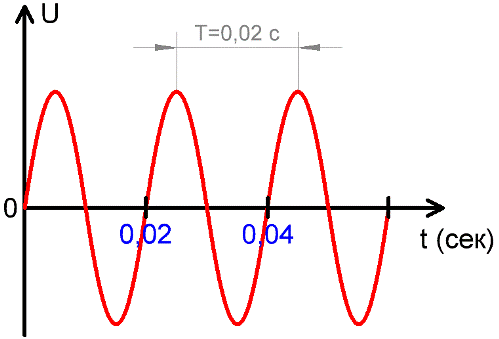
期間 — 振動しているシステムがすべての中間状態を通過し、再び初期状態に戻るまでにかかる時間。

交流の周期 T は、電流または電圧が 1 つの完全なサイクルで変化する時間間隔です。

交流電源は発電機であるため、周期は回転子の回転速度に関係し、発電機の巻線または回転子の回転速度が高くなるほど、生成される交流起電力の周期は短くなり、したがって、負荷の交流がわかります。

この周期は、この電流が考慮される特定の状況に応じて、秒、ミリ秒、マイクロ秒、ナノ秒で測定されます。上の図は、一定の特性周期 T を持ちながら、電圧 U が時間の経過とともにどのように変化するかを示しています。

周波数f

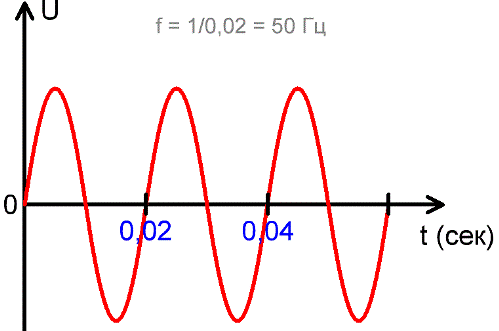
周波数 f は周期の逆数で、数値的には 1 秒間の電流​​または EMF 変化の周期数に等しくなります。つまり、f = 1 / T です。周波数の測定単位はヘルツ (Hz) です。これは、19 世紀の電気力学の発展に多大な貢献をしたドイツの物理学者ハインリヒ ヘルツにちなんで命名されました。期間が短いほど、EMF または電流変化の周波数が高くなります。

現在、ロシアでは、電力網の交流の標準周波数は 50 Hz です。つまり、1 秒間に網の電圧が 50 回変動します。

電気力学の他の分野では、より高い周波数が使用されます。たとえば、最新のインバーターでは 20 kHz 以上、電気力学のより狭い分野では最大数 MHz です。上の図では、1 秒間に 50 回の完全な振動があり、それぞれの持続時間は 0.02 秒で、1 / 0.02 = 50 であることがわかります。

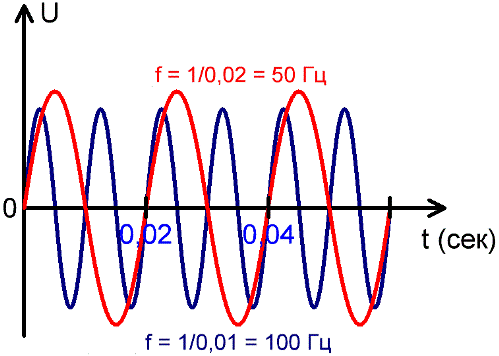
時間の経過に伴う正弦波交流の変化のグラフから、異なる周波数の電流には、同じ時間間隔内に異なる数の周期が含まれていることがわかります。

角周波数

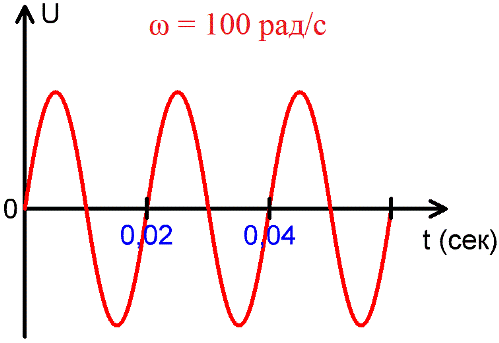
角周波数 — 2pi 秒間に行われる振動の数。

1 周期で、正弦波 EMF または正弦波電流の位相は 2pi ラジアンまたは 360 °変化します。したがって、交流正弦波電流の角周波数は次のようになります。

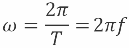
1秒単位ではなく、2π秒単位の発振回数を使用すると、高調波発振時の電圧と電流の変化の法則を表す式や、交流の誘導性や容量性の抵抗を表す式や、多くの式に使用できるため便利です。他の場合には、発振周波数 n が乗数 2pi とともに表示されます。

段階

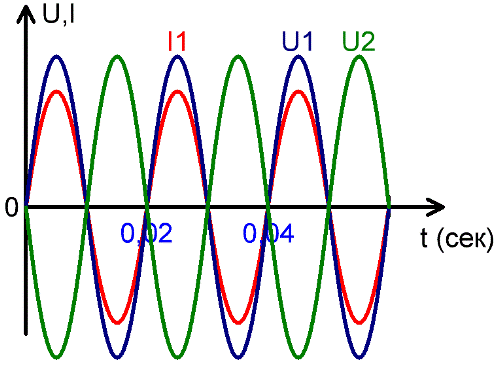
フェーズ — 定期的なプロセスの状態、段階。正弦波振動の場合、位相という用語はより明確な意味を持ちます。実際には、通常、役割を果たすのは位相自体ではなく、任意の 2 つの周期的プロセス間の位相シフトです。

この場合、「位相」という用語はプロセスの発展段階として理解され、この場合、交流電流と正弦波電圧に関連して、位相とは、ある瞬間における交流電流の状態と呼ばれます。時間。

これらの図は、電圧 U1 と電流 I1 の同相の一致、電圧 U1 と U2 の逆位相、および電流 I1 と電圧 U2 間の位相シフトを示しています。位相シフトはラジアン、周期の一部、度で測定されます。

以下も参照してください。 位相、位相角、位相シフトとは何ですか

振幅 Um と Im

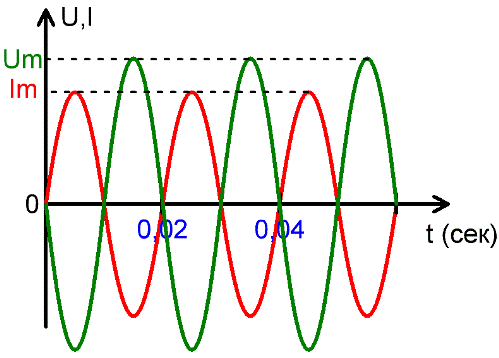
正弦波交流電流または正弦波交流起電力の大きさについて言えば、起電力または電流の最大値は振幅または振幅（最大）値と呼ばれます。

振幅 — 調和振動を行う量の最大値（たとえば、交流の電流強度の最大値、平衡位置からの振動振り子の偏差）、条件付きの特定の値からの振動量の最大偏差初期ゼロとして受け入れられます。

厳密に言えば、振幅という用語は正弦波振動のみを指しますが、通常は（完全に正確ではありませんが）上記の意味ですべての振動に適用されます。

オルタネーターについて話す場合、その端子の EMF は周期ごとに 2 回、正と負の半サイクル中にそれぞれ 1 回目は + Em、2 回目は Em の振幅値に達します。電流 I も同様に動作するため、Im で表されます。

調和振動 — 電気回路内の電圧などの振動量が、調和正弦波または余弦則に従って時間とともに変化する振動。正弦曲線でグラフで表現されます。

実際のプロセスは調和振動のみを近似できます。ただし、振動がプロセスの最も特徴的な特徴を反映している場合、そのようなプロセスは調和的であるとみなされ、多くの物理的および技術的問題の解決が大幅に促進されます。

調和振動に近い動きは、機械的 (振り子の振動)、音響的 (オルガン パイプ内の気柱の振動)、電磁的 (LC 回路内の振動) など、さまざまなシステムで発生します。振動理論は、物理的性質が異なるこれらの現象を統一的な観点から考察し、それらの共通の性質を決定します。

このベクトルに垂直で原点を通過する軸の周りを一定の角速度で回転するベクトルを使用して、調和振動をグラフで表すと便利です。ベクトルの回転角速度は、調和振動の円周周波数に対応します。

調和振動のベクトル図

あらゆる形式の周期プロセスは、異なる周波数、振幅、位相を持つ無限の一連の単純な調和振動に分解できます。

調和のとれた — 周波数が他の振動の周波数よりも整数倍大きい調和振動であり、基音と呼ばれます。高調波の番号は、その周波数が基本音の周波数の何倍であるかを示します (たとえば、第 3 高調波は、基本音の周波数の 3 倍高い周波数を持つ高調波振動です)。

周期的ではあるが調和的ではない（つまり、正弦波とは形状が異なる）振動は、調和振動、つまり基本音といくつかの高調波の合計として表すことができます。考慮されている振動の形式が正弦波と異なるほど、より多くの高調波が含まれます。

uとiの瞬時値

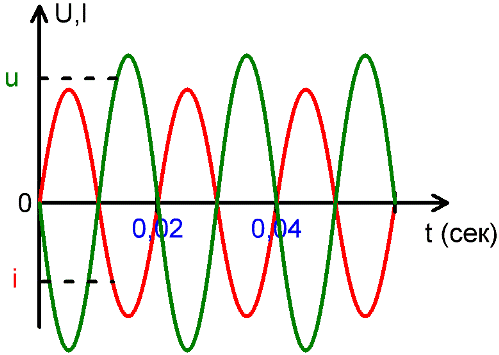
特定の瞬間における EMF または電流の値は瞬時値と呼ばれ、小文字の u および i で表されます。しかし、これらの値は常に変化するため、そこから AC 電流と EMF を推定するのは不便です。

I、E、Uの実効値

モーターのローターを機械的に回転させたり、加熱装置に熱を発生させたりするなど、有益な仕事を実行する交流の能力は、起電力と電流の実効値によって簡単に推定できます。

それで、 実効現在価値 は、検討中の交流の一周期中に導体を通過するときに、この交流と同じ機械的仕事または同じ量の熱を生成する直流電流の値と呼ばれます。

電圧、起電力、電流の RMS 値は、大文字 I、E、U で示されます。正弦波交流電流および正弦波交流電圧の実効値は次のとおりです。

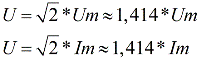
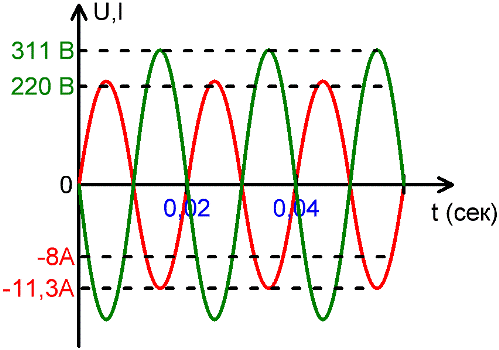
電気ネットワークを説明するには、電流と電圧の実効値を使用すると便利です。たとえば、220 ～ 240 ボルトの値は現代の家庭用コンセントの電圧の実効値であり、振幅はそれよりはるかに高く、311 ～ 339 ボルトです。

電流も同様で、例えば家庭用暖房器具に8アンペアの電流が流れるという場合、これは実効値を意味しますが、振幅は11.3アンペアです。

何らかの形で、電気設備における機械的仕事と電気エネルギーは、電圧と電流の実効値に比例します。測定装置の重要な部分は、電圧と電流の実効値を正確に示します。