電流と電圧の実効値

交流正弦波電流は、期間内で異なる瞬時値を持ちます。回路に含まれる電流計で測定される電流値はどのくらいになるのかという疑問が生じるのは自然なことです。

交流回路や電気測定を計算する場合、電流と電圧の瞬時値または振幅値を使用するのは不便であり、一定期間にわたる平均値はゼロになります。さらに、周期的に変化する電流の電気的影響 (放出される熱の量、完全な動作など) は、この電流の振幅によって推定することはできません。

最も便利なのは、電流と電圧のいわゆる実効値の概念の導入でした。これらの概念は、電流の方向に依存しない、電流の熱的（または機械的）作用に基づいています。

交流の二乗平均平方根値 - これは、交流期間中に交流中と同じ量の熱が導体に放出される直流電流の値です。

実行されたアクションを評価するには 交流電流、その作用を直流の熱効果と比較してみます。

抵抗rを通過する直流電力P A は、P = P2rとなります。

AC 電力は、全期間にわたる瞬時電力 Az2r の平均効果、または同じ時間の (I am x sinωT)2 NS r の平均として表されます。

期間の t2 の平均値を M とします。直流電力と交流電力を等しくすると、次のようになります。 Az2r = Mr -n より、Az = √M、

量 I は交流の実効値と呼ばれます。

交流における i2 の平均値は次のように求められます。

正弦波電流曲線を作成してみましょう。各瞬時電流値を二乗することにより、P 対時間曲線が得られます。

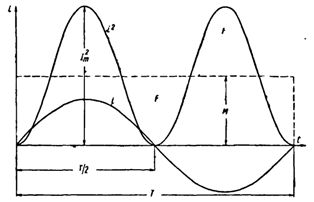AC実効値

期間の後半の負の電流 (-i) は 2 乗すると正の値になるため、この曲線の両方の半分は水平軸の上にあります。

底辺が T で、面積が曲線 i2 と横軸で囲まれた面積に等しい長方形を作成します。長方形の高さ M は、その期間の P の平均値に対応します。高等数学を使用して計算されたこの周期値は、1/2 I2m に等しくなります... したがって、M. = 1/2 I2m

交流の実効値 Im は Im = √M なので、最終的に I = Im / √2 となります。

同様に、電圧 U と E の実効値と振幅値の関係は次の形式になります。

U = うーん / √2E = エム / √2

変数の実効値は、下付き文字なしの大文字 (I、U、E) で示されます。

上記に基づいて、交流の実効値は、交流と同じ抵抗を通過して同じ量のエネルギーを同時に放出する直流に等しいと言えます。

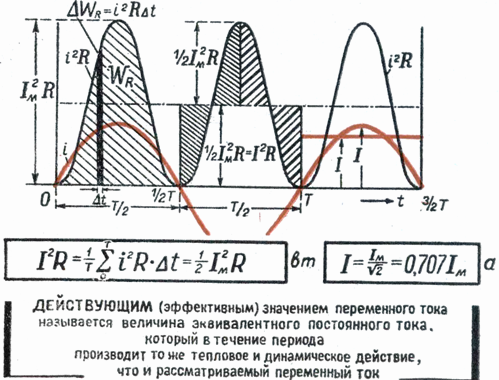
交流回路に含まれる電気計測器（電流計、電圧計）は、電流または電圧の実効値を示します。

ベクトル図を作成するときは、振幅ではなくベクトルの実効値を延期する方が便利です。このため、ベクトルの長さは 1 回 √2 減らされます。これによって、図上のベクトルの位置は変わりません。