AC回路における過渡現象、転流則、共振現象

電気回路の定常動作モードは、回路内のパラメータ（電圧、電流、抵抗など）が一定であるモードです。定常状態に達した後に電圧が変化すると、電流も変化します。ある定常状態から別の定常状態への移行はすぐには起こりませんが、一定の時間がかかります (図 1)。

ある定常状態から別の定常状態への遷移中に回路内で発生するプロセスは、過渡状態と呼ばれます。過渡現象は、回路パラメータが突然変化すると発生します。電気回路の動作モードが突然変化した瞬間を最初の瞬間とし、それを基準にして回路の状態を特徴付け、過渡プロセス自体を説明します。

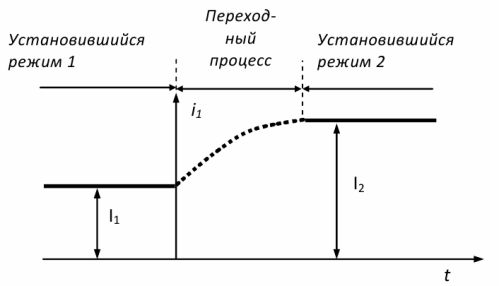
米。 1. 交流回路で発生するモード

過渡プロセスの継続時間は非常に短く、数分の一秒で計算できますが、プロセスを特徴付ける電流と電圧、またはその他のパラメータは大きな値に達する可能性があります。過渡現象は、回路内の転流によってトリガーされます。

整流とは、スイッチング デバイスの接点を開閉することです。過渡現象を解析する場合、2 つの整流則が使用されます。

交換の第一法則: 電流。スイッチング前にインダクタに流れる電流は、スイッチング直後に同じコイルに流れる電流と等しくなります。これらは。インダクタ内の電流は急激に変化することはできません。

転流の第 2 法則: スイッチング前の容量性素子の両端の電圧は、スイッチング後の同じ素子の両端の電圧に等しい。これらは。容量性要素の両端の電圧は急激に変化することはできません。抵抗、インダクタ、およびコンデンサの直列接続の場合、依存関係は有効です

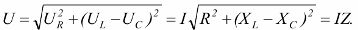
同じ反応 Xl と Xc を考慮した回路では、いわゆる電圧共振が発生します。これらの抵抗は周波数に依存するため、ある共振周波数 ω® で共振が発生します。

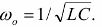
この場合の回路の合計抵抗は最小限であり、純粋にアクティブです。 Z = R であり、電流には最大値があります。 ω ωо では、負荷は能動容量性の特性を持ち、ω >ωо では能動誘導性になります。

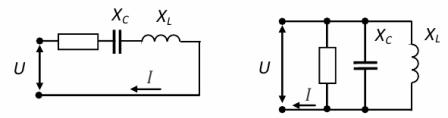
共振時の回路内の電流の急激な増加は、Xl と Xc の増加に対応することに注意してください。これらのストレスは電圧よりもはるかに大きくなる可能性があります。回路端子に U が適用されるため、電圧共振は電気設備にとって危険な現象です。

並列接続された回路要素の分岐内の電流は、回路全体の電圧に対して対応する位相シフトを持ちます。したがって、回路の合計電流は、位相シフトを考慮した個々の分岐の電流の合計に等しく、次の式で決定されます。

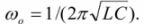
リアクタンス Xl と X が等しい場合、素子を並列接続した回路では共振電流が発生します... 共振電流は最大値および最大力率 (cosφ = 1) に達します。共振周波数の値は次の式で求められます。

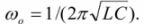
共振時の L と C を含む分岐の電流は、回路の合計電流よりも大きくなる可能性があります。誘導電流と容量電流は逆位相で、値が等しく、電源に対して相互にオフセットします。これらの回路では、誘導コイルとコンデンサの間でエネルギーが交換されます。

電流の共振に近いモードは、電力消費者の力率を高めるために広く使用されています。これにより、ワイヤの荷降ろし、損失の削減、材料とエネルギーの節約により、大きな経済効果が得られます。