ACコンデンサ

で回路を組み立ててみましょう コンデンサ、オルタネーターは正弦波電圧を生成します。スイッチを閉じると回路内で何が起こるかを順番に分析してみましょう。発電機の電圧がゼロに等しい最初の瞬間を考えます。

期間の最初の 4 分の 1 では、発電機の端子間の電圧がゼロから増加し、コンデンサが充電され始めます。回路内に電流が発生しますが、コンデンサを充電する最初の瞬間では、プレート上の電圧が現れたばかりでまだ非常に小さいという事実にもかかわらず、回路内の電流（充電電流）が最大になります。 。コンデンサの電荷が増加すると、回路内の電流が減少し、コンデンサが完全に充電された瞬間にゼロに達します。この場合、コンデンサのプレート上の電圧は、発電機の電圧に厳密に従って、この時点で最大になりますが、符号が逆になります。つまり、電圧は発電機の電圧に向けられます。

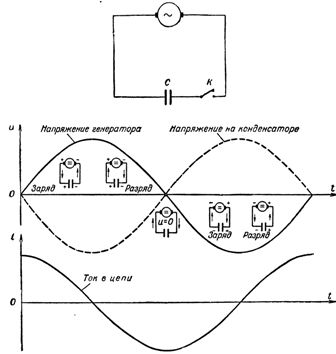
米。 1. 容量のある回路における電流と電圧の変化

このように、電流は最大の力でコンデンサに自由に流れ込みますが、コンデンサのプレートが電荷で満たされるとすぐに減少し始め、ゼロに低下して完全に充電されます。

この現象を、一方が満水でもう一方が空である 2 つの連絡容器 (図 2) を接続するパイプ内で起こる水の流れと比較してみましょう。水路を遮断するバルブを押すだけで、すぐに水が大きな圧力で左側の容器からパイプを通って空の右側の容器に流れ込みます。しかし、すぐに、容器内のレベルが均等になるため、パイプ内の水圧は徐々に弱まり始め、ゼロに低下します。水の流れが止まります。

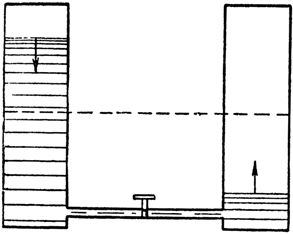
米。 2. 通信容器を接続する配管内の水圧の変化は、コンデンサの充電時の回路内の電流の変化に似ています。

同様に、電流は最初に充電されていないコンデンサに流れ込み、充電されるにつれて徐々に弱まります。

期間の第 2 四半期が始まり、発電機の電圧が最初はゆっくりと始まり、その後ますます急速に減少すると、充電されたコンデンサが発電機に放電し、回路内に放電電流が発生します。発電機の電圧が低下すると、コンデンサの放電が増加し、回路内の放電電流が増加します。期間のこの 4 分の 1 における放電電流の方向は、期間の最初の 4 分の 1 における充電電流の方向と逆になります。したがって、ゼロ値を通過した電流曲線は時間軸の下に位置します。

最初の半サイクルの終わりまでに、発電機の電圧とコンデンサの電圧は急速にゼロに近づき、回路電流はゆっくりと最大値に達します。回路内の電流の値が大きくなるほど、回路内を流れる電荷の値も大きくなることを考えると、コンデンサのプレートの電圧が上昇し、したがって電荷が上昇したときに電流が最大に達する理由が明らかになるでしょう。コンデンサーが急激に減少します。

期間の第 3 四半期が始まると、コンデンサは再び充電を開始しますが、そのプレートの極性と発電機の極性が変わり、「逆も同様で、電流は同じ状態で流れ続けます」コンデンサが充電されるにつれて減少し始め、期間の第 3 四半期の終わり、発電機とコンデンサの電圧が最大値に達すると、電流はゼロになります。

期間の最後の 4 分の 1 では、電圧は減少してゼロに下がり、回路内で方向が変わった電流は最大値に達します。ここでピリオドが終了し、その後次のピリオドが始まり、前のピリオドを正確に繰り返します。

したがって、発電機の交流電圧の作用により、コンデンサは期間中に 2 回充電され (期間の第 1 四半期と第 3 四半期)、2 回放電されます (期間の第 2 四半期と第 4 四半期)。でも、一つずつ交互に入れていくので、 コンデンサの充電と放電 回路内を充電および放電電流が流れるたびに、次のように結論付けることができます。 交流電流.

これは次の簡単な実験で確認できます。 25 W の電球を介して 4 ～ 6 マイクロファラッドのコンデンサを主電源に接続します。ライトは点灯し、回路が切断されるまで消えません。これは、静電容量のある回路に交流電流が流れたことを示しています。もちろん、電流はコンデンサの誘電体を通過しませんが、いつでも充電電流またはコンデンサの放電電流を表します。

ご存知のとおり、コンデンサが充電されると誘電体に生じる電界の作用により誘電体が分極し、コンデンサが放電すると分極が消失します。

この場合、変位電流が発生する誘電体は、交流に対しては一種の回路の継続として機能し、定数に対しては回路を遮断します。しかし、変位電流はコンデンサの誘電体内でのみ形成されるため、回路に沿った電荷の移動は起こりません。

AC コンデンサによってもたらされる抵抗は、コンデンサの静電容量の値と電流の周波数によって異なります。

コンデンサの容量が大きいほど、コンデンサの充電および放電中に回路にかかる電荷が大きくなり、したがって回路内の電流も大きくなります。回路内の電流の増加は、その抵抗が減少したことを示します。

したがって、静電容量が増加すると、交流に対する回路の抵抗が減少します。

成長しています 電流周波数 コンデンサの充電（および放電）は低周波数よりも速く行われる必要があるため、回路内で運ばれる電荷の量が増加します。同時に、単位時間あたりに転送される電荷​​量の増加は回路内の電流の増加に相当し、したがって回路の抵抗が減少することになります。

何らかの方法で交流の周波数を徐々に下げて電流を直流にすると、回路に含まれるコンデンサの抵抗が徐々に増加して無限に大きくなり（回路が破壊され）、 定電流回路.

したがって、周波数が高くなると、交流に対するコンデンサの抵抗は減少します。

交流に対するコイルの抵抗を誘導性と呼ぶのと同じように、コンデンサの抵抗を容量性と呼びます。

したがって、回路の容量とそれに供給される電流の周波数が低いほど、容量性抵抗は大きくなります。

容量抵抗は Xc で示され、オーム単位で測定されます。

電流の周波数と回路の容量に対する容量性抵抗の依存性は、式 Xc = 1 /ωC によって決定されます。ここで、ω は 2πe の積に等しい円周周波数、C は回路の容量です。ファラド。

コンデンサは電流源のエネルギーを消費しないため、容量性抵抗は、誘導性抵抗と同様に反応性の性質を持っています。

方式 オームの法則 容量性回路の場合、I = U / Xcの形式になります。IとUは電流と電圧の実効値です。 Xc は回路の容量性抵抗です。

コンデンサは低周波電流に強く、高周波電流を通しやすい性質を持っているため、通信機器の回路に広く使われています。

たとえば、コンデンサの助けを借りて、回路の動作に必要な定電流および低周波電流を高周波電流から分離することができます。

回路の高周波部分で低周波電流の経路を遮断する必要がある場合は、小さなコンデンサを直列に接続します。低周波電流に対する耐性が高く、同時に高周波電流を容易に通過させます。

たとえば、無線局の電源回路で高周波電流を防ぐ必要がある場合は、電流源と並列に接続された大容量のコンデンサが使用されます。この場合、高周波電流は無線局の電源回路をバイパスしてコンデンサを通過します。

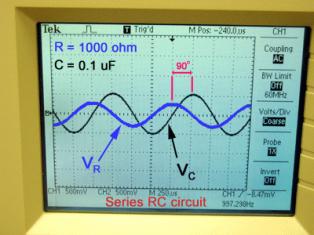
AC回路のアクティブ抵抗とコンデンサ

実際には、静電容量を有する直列回路にある場合がよく観察されます。 アクティブ抵抗が含まれています。 この場合の回路の合計抵抗は次の式で求められます。

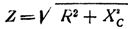
したがって、アクティブ AC 抵抗と容量性 AC 抵抗で構成される回路の合計抵抗は、この回路のアクティブ抵抗と容量性抵抗の二乗の合計の平方根に等しくなります。

オームの法則は、この I = U / Z 回路にも当てはまります。

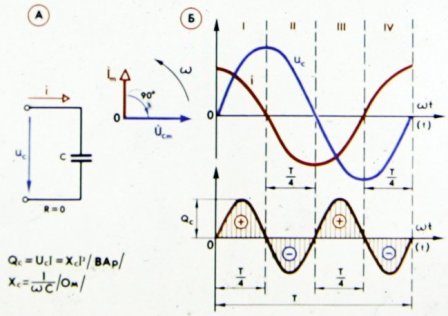
図では。図３は、容量性抵抗と能動抵抗を含む回路における電流と電圧の間の位相関係を特徴付ける曲線を示している。

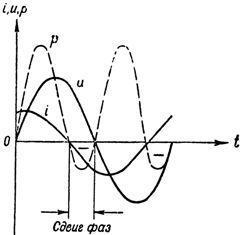
米。 3. コンデンサとアクティブ抵抗を備えた回路の電流、電圧、電力

図からわかるように、この場合の電流は電圧を周期の 4 分の 1 ずつ増加させるのではなく、それよりも少なく増加させます。これは、位相の減少によって明らかなように、アクティブ抵抗が回路の純粋な容量性 (無効性) の性質に違反するためです。シフト。ここで、回路端子の電圧は 2 つの成分の合計として定義されます。電圧の無効成分は回路の容量性抵抗を克服し、電圧の有効成分はその活性抵抗を克服します。

回路のアクティブ抵抗が大きいほど、電流と電圧の間の位相シフトは小さくなります。

回路内の電力変化の曲線 (図 3 を参照) は、期間中に 2 回負の符号を取得しました。これは、すでに知られているように、回路の反応性の性質の結果です。回路の反応性が低いほど、電流と電圧の間の位相シフトが小さくなり、回路が消費する電流源電力が増加します。

こちらもお読みください: 電圧共振