電動機の機械的特性と生産機構

電気駆動装置を設計するときは、その機械的特性が生産機構の機械的特性と一致するように電気モーターを選択する必要があります。機械的特性は、定常状態における変数の関係を示します。

機構の機械的特性は、角速度と機構の抵抗モーメント (モーター軸に換算) ω = f (Mc) の関係と呼ばれます。

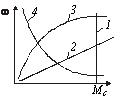
米。 1. 機構の機械的特性

すべての種類の中で、メカニズムの機械的特性にはいくつかの特徴的なタイプがあります。

1. 速度に依存しない抵抗モーメントを持つ特性（図1の直線1）。速度に依存しない機械的特性は、回転軸に平行な直線 (この場合は垂直) として描かれます。このような特性は、たとえばクレーン、ウインチ、吐出高さが一定のピストンポンプなどに備わっています。

2.抵抗モーメントが速度に線形に依存する特性 (図 1 の 2 行目)。この依存性は、たとえば、一定の負荷で動作する独立励磁 DC 発電機の駆動に固有のものです。

3. トルクが非線形に増加する特性 (図 1 の曲線 3)。典型的な例は、ファン、遠心ポンプ、プロペラの動作です。これらの機構では、モーメント Mc は角速度 ω の 2 乗に依存します...これはいわゆるパラボリック（ファン）の機械的特性。

4. 抵抗モーメントが非線形に減少する特性 (図 1 の曲線 4)。ここで、抗力モーメントは回転速度に反比例します。この場合、動力は機構の動作速度範囲全体にわたって一定に保たれます。例えば、一部の金属切削機械（旋削、フライス、穴あけ）の主な動作機構では、モーメントMcがωに反比例して変化し、機構が消費する電力は一定となります。

電気モーターの機械的特性は、トルクに対する角速度の依存性 ωd = f (M) と呼ばれます。ここで、モーターシャフトのモーメント M は、回転方向に関係なく、正の符号、つまり移動モーメントを持っていることに留意する必要があります。同時に、抵抗モーメント Mc は負の符号を持ちます。

例として、図 1 に示します。図 2 は機械的特性を示しています。 1 - 同期モーター。 2 — 独立した励磁を備えた DC モーター。 3 — 直列励磁を備えた DC モーター。

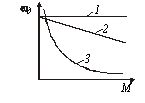米。 2. 電動機の機械的特性

電気駆動装置の機械的特性を評価するには、特性剛性の概念が使用されます。機械的特性の剛性は次の式で求められます。

β = dM / dω

ここで、dM - エンジントルクの変化。 dωd — 対応する角速度の変化。

線形特性の場合、値 β は一定のままですが、非線形の場合、β 値は動作点に依存します。

この概念を使用すると、図に示す機能が得られます。 2 は次のように定性的に評価できます。 1 — 絶対的に剛体 (β = ∞)。 2 — 固体。 3 — 柔らかい。

非常に難しい特性です。モーター負荷がゼロから公称値に変化しても、モーター回転速度は変化しません。同期モーターにはこのような特性があります。

剛性特性 — 負荷がゼロから公称値に変化しても、回転速度はほとんど変化しません。この特性は、特性の線形部分の領域では、並列励磁 DC モータだけでなく誘導モータにも備わっています。

リジッド特性とは、負荷をゼロから定格まで変化させたときの速度変化が定格速度の約10％を超えない特性と考えられます。

ソフトな特性 — 負荷の比較的小さな変化でモーター速度が大きく変化します。この特性は、直列、混合、または並列励磁を備えた直流モーターが備えていますが、電機子回路に追加の抵抗があり、ローター回路の抵抗と非同期です。

ほとんどの生産機構には、堅牢な機械的特性を持つ非同期かご型モーターが使用されます。

電気モーターのすべての機械的特性は、自然と人工に分けられます。

自然な機械的特性とは、パラメータの公称値によるエンジンの動作条件を指します。

たとえば、並列励磁モーターの場合、電機子電圧と励磁電流が公称値であり、電機子回路に追加の抵抗がない場合の自然特性をプロットできます。

誘導モーターの固有の特性は、ローター回路に追加の抵抗がない場合、モーターのステーターに供給される交流の定格電圧と定格周波数に対応します。

したがって、各エンジンに対して構築できる自然特性は 1 つだけであり、人工特性は無制限に構築できます。たとえば、DC モーターの電機子抵抗や誘導モーターの回転子回路の各新しい値には、独自の機械的特性があります。