磁気回路のオームの法則

もし磁束がなかったら、現代の電気工学は存在しなかったでしょう。発電機と電気モーター、電磁石と変圧器、測定器とホール センサーの動作は、磁場の使用と磁束の特性に基づいています。

磁束を集中させて強化するために、強磁性材料を使用します。強磁性体が生成される 磁気コア — 必要な形状とサイズの本体、任意のサイズの磁束を必要な方向に向けるためのコア。閉じた磁気誘導線が内部を通過するこのような物体は、磁気回路と呼ばれます。

磁場の既知の特性により、さまざまな磁気回路内の磁束を計算することが可能になります。しかし、実際の作業では、これらの法則を毎回直接使用するよりも、磁場の法則から導出される磁気回路の一般的な結果と法則に頼るほうがはるかに便利です。磁気回路に特定のルールを適用すると、典型的な実際的な問題を解決するのに便利です。

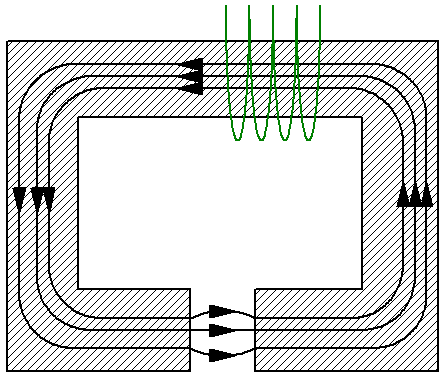
たとえば、断面 S の非分岐ヨークで構成される単純な磁気回路を考えてみましょう。ヨークは次のような材料で作られています。 透磁率μ… ヨークには同じ面積 S の非磁性ギャップ、たとえば空気があり、ギャップ内の透磁率 — mu1 — はヨークの透磁率とは異なります。ここで、平均誘導線を調​​べて、磁気張力定理をそれに適用できます。

磁気誘導線は回路全体で連続しているため、ヨークとギャップの磁束の大きさは同じになります。ここで次の式を使用します。 磁気誘導 B、磁束 F は磁場の強さ H を磁束 F で表します。

次のステップでは、得られた式を上記の磁束定理の式に代入します。

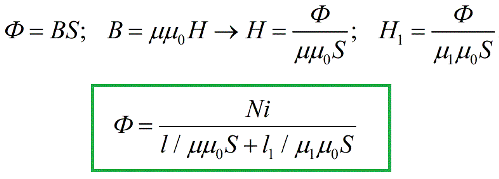
電気工学で知られている式と非常によく似た式が得られました。 閉回路の一部に関するオームの法則ここでの EMF の役割は、起電力から類推して起磁力 (または MDF) と呼ばれる量 iN によって演じられます。 SI システムでは、起磁力はアンペアで測定されます。

分母の合計は電気回路の全電気抵抗のアナロジーにすぎず、磁気回路の場合はそれに応じて全磁気抵抗と呼ばれます。分母の項は、磁気回路の個々のセクションの磁気抵抗です。

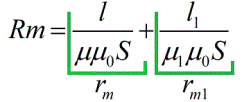
磁気抵抗は、磁気回路の長さ、断面積、および透磁率 (通常のオームの法則の導電率と同様) に依存します。その結果、磁気回路についてのみオームの法則の式を書くことができます。

つまり、磁気回路に関するオームの法則の定式化は次のようになります。「分岐のない磁気回路では、磁束は MDS を回路の全磁気抵抗で割った商に等しい。」

式から明らかなように、磁気抵抗は 北東で はウェーバーアンペアで測定され、磁気回路の合計磁気抵抗は、磁気回路の各部分の磁気抵抗の合計に数値的に等しくなります。

説明した状況は、磁束がこれらすべての部品を連続的に貫通する限り、任意の数の部品を含む分岐していない磁気回路に当てはまります。磁気コアが直列に接続されている場合、全体の磁気抵抗は各部品の磁気抵抗を加算することによって求められます。

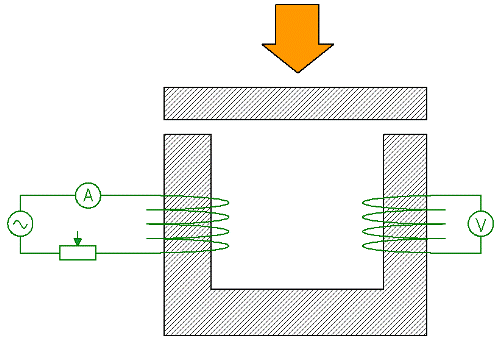
回路の各部分の磁気抵抗が回路の全体の磁気抵抗に及ぼす影響を実証する実験について考えてみましょう。U 字型の磁気回路はコイル 1 によって磁化され、コイル 1 は電流計と加減抵抗器を介して (交流) 供給されます。 EMF は二次巻線 2 に誘導され、ご存知のとおり、巻線に接続された電圧計の測定値は磁気回路内の磁束に比例します。

ここで加減抵抗器で一次巻線の電流を一定に保ち、同時に鉄板を上の磁気回路に押し付けると、回路の合計磁気抵抗が大幅に減少した後、それに応じて電圧計も増加します。

もちろん、「磁気抵抗」や「起磁力」などの上記の用語は形式的な概念です。磁束の中には何も移動せず、移動する粒子も存在しないため、それは単なる視覚的表現（流体の流れモデルのような）にすぎません。法律をより明確に理解する...

上記の実験および他の同様の実験の物理的意味は、磁気回路への非磁性ギャップや磁性材料の導入が磁気回路内の磁束にどのような影響を与えるかを理解することです。

たとえば、磁気回路に磁石を導入することにより、回路内にすでに含まれている物体に追加の分子電流が追加され、追加の磁束が導入されます。 「磁気抵抗」や「起磁力」などの形式的な概念は、実際の問題を解決するときに非常に便利であることが証明されており、電気工学でうまく使用されているのはこのためです。