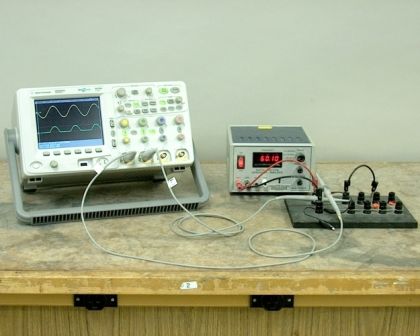
インパルス電流
さまざまな電子機器、たとえば電子および半導体機器、つまり増幅器、整流器、ラジオ、発電機、テレビ、カーボンマイク、電信機、その他多くの機器において、リップル電流と電圧は広く使用されています。推論を二度繰り返さないように、電流についてのみ説明しますが、電流に関連するすべてのことは電圧にも当てはまります。
方向は一定だが値が変化する脈流は、異なる場合があります。現在の値がゼロ以外の最高値から最低値に変化する場合があります。他の場合には、電流はゼロに減少します。もしも 直流回路 特定の周波数で遮断されると、しばらくの間、回路に電流が流れなくなります。
図では。図１は、様々な波流のグラフを示す。図では。 1、a、b、電流の変化は次のように発生します。 正弦曲線、ただし、電流の方向 (符号) は変わらないため、これらの電流を正弦波交流と見なすべきではありません。図では。図１のｃは、別々のパルス、すなわち、長短の休止によって互いに分離された電流の短命「ショック」からなる電流を示し、しばしばパルス電流と呼ばれる。異なるパルス電流は、パルスの形状と持続時間、および繰り返し率が互いに異なります。
あらゆる種類の脈動電流は、項電流または成分電流と呼ばれる、直流と交流の 2 つの電流の合計と考えると便利です。脈動電流には DC 成分と AC 成分が含まれます。これは多くの人にとって奇妙に思えます。実際、結局のところ、脈動電流は常に一方向に流れ、その値が変化する電流です。
方向を変える交流が含まれているとどうやって判断できますか?しかし、同じ電線に直流と交流の 2 つの電流が同時に流れると、その電線には脈動電流が流れることがわかります (図 2)。この場合、交流電流の振幅は直流電流の値を超えてはなりません。直流電流と交流電流を別々にワイヤに流すことはできません。これらは、脈動電流のすべての特性を備えた一般的な電子の流れに追加されます。
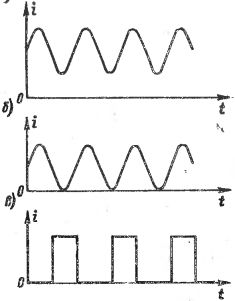
米。 1. 各種波流のグラフ
AC 電流と DC 電流の加算をグラフで表示できます。図では。図２は、１５ｍＡに等しい直流電流と振幅１０ｍＡの交流電流のグラフを示す。電流の方向（符号）を考慮して、各時点のこれらの電流の値を合計すると、図に示す波流グラフが得られます。 2 太線で示します。この電流は、最低 5 mA から最高 25 mA まで変化します。
電流の加算を考慮すると、脈流を直流電流と交流電流の合計として表すことの妥当性が確認されます。この表現の正確さは、いくつかのデバイスの助けを借りて、この電流の成分を互いに分離できるという事実によっても確認されます。
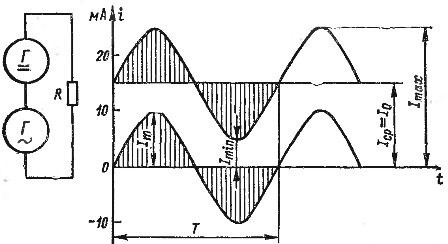
米。 2. 直流と交流を加算して脈流を得る。
いかなる電流も常に複数の電流の合計として表すことができることを強調しておく必要があります。たとえば、5 A の電流は、一方向に流れる電流 2 と 3 A の合計、または異なる方向に流れる電流 8 と 3 A の合計、つまり、電流 8 の差であると考えることができます。合計 5 A を与える 2 つ以上の電流の他の組み合わせを見つけることは難しくありません。
ここでは、力の加算と分解の原理と完全に類似しています。 2 つの同じ向きの力が任意の物体に作用する場合、それらは 1 つの共通の力で置き換えることができます。反対方向に働く力は単位の違いで置き換えることができます。逆に、与えられた力は常に、対応する同じ方向の力の合計、または反対方向の力の差であると考えることができます。
直流または正弦波交流を成分電流に分解する必要はありません。脈流を直流電流と交流電流の合計に置き換えると、これらの成分電流に直流電流と交流電流の既知の法則を適用することで、多くの問題を解決し、脈流に関連する必要な計算を行うことができます。
脈流は直流電流と交流電流の合計であるという概念が一般的です。もちろん、特定の時間間隔で、直流電流と交流電流が実際に電線に沿って互いに向かって流れるとは想定できません。実際、電子の流れは 2 つと逆ということはありません。
実際には、脈動電流は時間の経過とともに値が変化する単一の電流です。脈動電圧または脈動起電力は、定数成分と変動成分の合計として表すことができると言ったほうが正確です。
例えば、図１では、図 2 は、ある発電機の定数 emf が別の発電機の変数 emf に代数的にどのように加算されるかを示しています。その結果、対応する脈動電流を引き起こす脈動 EMF が発生します。ただし、条件付きでは、定EMFは回路内に直流を生成し、交流EMFは合計すると脈動電流を形成する交流であると考えることができます。
各脈動電流は、Itax と Itin の最大値と最小値、およびその定数成分と可変成分によって特徴付けることができます。定数成分は I0 で示されます。交流成分が正弦波電流の場合、その振幅は It で表されます (これらすべての量は図 2 に示されています)。
It と Itax を混同しないでください。また、電流波形の最大値 Imax を振幅と呼ぶべきではありません。振幅という用語は通常、交流のみを指します。脈流に関しては、その変動成分の振幅についてのみ説明できます。
脈流の一定成分をその平均値Ｉａｖ、すなわち算術平均値と呼ぶことができる。実際、図に示した脈流の一周期の変化を考えてみると、図 2 を見ると、次のことがはっきりとわかります。最初の半サイクルでは、電流成分を 0 から 10 mA まで変化させて 0 に戻すことで、15 mA の電流に多くの値が追加され、後半では、 -サイクル、まったく同じ電流値が電流15mAから減算されます。
したがって、15mA という電流は実際には平均値です。電流はワイヤの断面を通した電荷の移動であるため、Iav は、1 周期 (または整数周期) でこの脈動電流と同じ量の電気を流すような直流電流の値です。 。
正弦波交流の場合、ある半周期で導体の断面を通過する電気量は、別の半周期で反対方向に通過する電気量に等しいため、周期ごとの Iav の値はゼロです。電流 i の時間 t への依存性を示す電流のグラフでは、電流によって運ばれる電気量は電流曲線で囲まれた図の面積で表されます。これは、電気量は次の式で決まるからです。商品それとなります。
正弦波電流の場合、正と負の半波の面積は等しくなります。図２に示すように、前半期間では、電流Ｉａｖの電気量に交流成分の電気量が加算される（図中の斜線部）。そして、後半のサイクルでは、まったく同じ量の電気が取り出されます。その結果、単一の直流電流 Iav の場合と同じ量の電気が全期間を通じて転送されます。つまり、長方形 Iav T の面積は、波流曲線によって境界付けられる面積に等しくなります。
したがって、電流の一定成分または平均値は、ワイヤの断面を通る電荷の移動によって決まります。
図に示す電流方程式は次のようになります。 2 は明らかに次の形式で記述する必要があります。
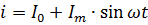
脈動電流の電力は、その成分電流の電力の合計として計算する必要があります。たとえば、図のような電流が流れた場合、 2、抵抗 R の抵抗を通過すると、その電力は次のようになります。
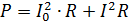
ここで、I = 0.7Im は可変成分の実効値です。
波流電流 Id の実効値の概念を導入できます。電力は通常の方法で計算されます。
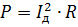
この式を前の式と同等にして R で簡約すると、次のようになります。
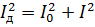
応力についても同様の関係が得られます。