電界特性
この記事では、電場の主な特性である電位、電圧、強度について説明します。
電場とは何ですか
電場を生成するには、電荷を生成する必要があります。電荷の周囲の空間（帯電物体）の性質は、電荷のない空間の性質とは異なります。同時に、空間に電荷が導入されても、空間の性質は即座には変化しません。変化は電荷から始まり、空間内のある点から別の点まで一定の速度で広がります。
電荷を含む空間では、その空間に導入された他の電荷に作用する機械的な力が現れます。これらの力は、ある電荷が別の電荷に直接作用した結果ではなく、質的に変化した媒体を介した作用の結果です。
電荷の周囲に導入された電荷に作用する力が現れる空間を電場といいます。
電界内の電荷は、電界の側からそれに作用する力の方向に移動します。このような電荷の静止状態は、電場の強さと釣り合う何らかの外部（外部）の力が電荷に加えられた場合にのみ可能です。
外力と場の強さのバランスが崩れるとすぐに、電荷は再び動き始めます。その動きの方向は常に、より大きな力の方向と一致します。
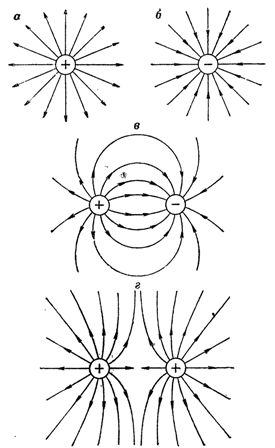
わかりやすくするために、電場は通常、いわゆる電力線で表されます。これらの線は、電場に作用する力の方向と一致します。同時に、線に垂直に設置された領域の1cm2ごとの線の数が、対応する点の場の強度に比例するように、非常に多くの線を引くことが合意されました。
場の方向は通常、特定の場に置かれた正電荷に作用する場の強さの方向であると見なされます。プラスの電荷はプラスの電荷には反発し、マイナスの電荷には引き付けられます。したがって、電界は正電荷から負電荷に向けられます。
力線の方向は、図面では矢印で示されている。科学は、電界の力線には始まりと終わりがあること、つまり、電界の力線は自然に閉じないことを証明しました。想定される場の方向に基づいて、力線は正の電荷 (正に帯電した物体) で始まり、負の電荷で終わることがわかります。
米。 1. 力線を使用した電場の画像の例: a — 単一の正電荷を持つ電場、b — 単一の負電荷を持つ電場、c — 2 つの反対の電荷を持つ電場、d — 2つの同様の電荷の電場
図では。図１は、力線を使用して描かれた電場の例を示す。電気力線は場をグラフィックで表現する手段にすぎないことを覚えておく必要があります。ここでの力線の概念にとって、これ以上の本質はありません。
クーロンの法則
2 つの電荷間の相互作用の強さは、電荷のサイズと相互配置、およびそれらの環境の物理的特性によって決まります。
2 つの電気を帯びた物理的な物体の場合、その寸法は物体間の距離に比べて取るに足らないものですが、相互作用の治癒は次のように数学的に決定されます。
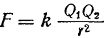
ここで、F は電荷の相互作用の力 (ニュートン (N))、k — 電荷間の距離 (メートル)、Q1 と Q2 — 電荷の大きさ (クーロン (k))、k は比例係数です。電荷を取り囲む媒体の特性に依存します。
上の式は次のようになります。2 つの点電荷間の相互作用の力は、これらの電荷の大きさの積に正比例し、それらの間の距離の 2 乗に反比例します (クーロンの法則)。
比例係数 k を決定するには、式 k = 1 /(4πεεО) を使用します。
電界ポテンシャル
電荷に作用する場の力が外力によってバランスが取れていない場合、電場は常に電荷に動きを与えます。これは、電場には位置エネルギー、つまり仕事をする能力があることを意味します。
電荷を空間内のある点から別の点に移動させると、電場が実際に機能し、その結果、場への位置エネルギーの供給が減少します。電場内で電荷が、場の力と反対に作用する何らかの外力の作用下で移動する場合、仕事は電場の力ではなく、外力によって行われます。この場合、場の位置エネルギーは減少しないだけでなく、逆に増加します。
電場内で電荷を移動させる外力によって行われる仕事は、その動きに対抗する場の力の大きさに比例します。この場合、外力によって行われる仕事は、場の位置エネルギーの増加に完全に費やされます。ポテンシャルエネルギーの側面から場を特徴付けるために、電場ポテンシャルと呼ばれる量が呼び出されます。
この量の本質は次のとおりです。正電荷が検討中の電場の外側にあると仮定します。これは、フィールドが特定の電荷に実質的に影響を及ぼさないことを意味します。外力によってこの電荷が電場に導入され、場の力によって加えられる動きに対する抵抗を克服して、電荷が場の特定の点に移動します。力によって行われる仕事、したがって場の位置エネルギーが増加する量は、完全に場の特性に依存します。したがって、この研究により、特定の電場のエネルギーを特徴付けることができます。
場の所定の点に置かれた正電荷の単位に関連する電場エネルギーは、所定の点における電場ポテンシャルと呼ばれます。
ポテンシャルを文字 φ で、電荷を文字 q で、電荷を移動させるのに費やされる仕事を W で表すと、ある点における場のポテンシャルは式 φ = W / q で表されます。
したがって、所定の点における電場のポテンシャルは、単位正電荷が電場から所定の点に向かって移動するときに外力によって行われる仕事に数値的に等しいということになります。フィールド電位はボルト (V) 単位で測定されます。場の外の所定の点に 1 クーロンの電気が伝達される間に、外力が 1 ジュールに等しい仕事をした場合、場の所定の点の電位は 1 ボルトに等しくなります。 1 ボルト = 1 ジュール / 1クーロン
電界強度
どのような電場でも、正電荷は電位の高い点から電位の低い点に移動します。逆に、マイナス電荷は電位の低い点から電位の高い点に移動します。どちらの場合も、仕事は電場の位置エネルギーを犠牲にして行われます。
この仕事、つまり正電荷 q が場の点 1 から点 2 に移動するときに場の位置エネルギーが減少する量がわかれば、これらの点間の電圧を見つけるのは簡単です。フィールド U1、2:
U1,2 = A / q、
ここで、A は、電荷 q が点 1 から点 2 に移動するときに場の力によって行われる仕事です。電場の 2 点間の電圧は、単位正電荷を 1 つの点から移動するためにゼロによって行われる仕事に数値的に等しくなります。フィールドで別の人に。
ご覧のとおり、場の 2 点間の電圧と同じ点間の電位差は同じ物理単位を表します。したがって、電圧と電位差という用語は同じです。電圧はボルト (V) 単位で測定されます。
1 クーロンの電気を磁場のある点から別の点に伝達するときに、磁場の力が 1 ジュールに等しい働きをする場合、2 点間の電圧は 1 ボルトに等しくなります。 1 ボルト = 1 ジュール / 1 クーロン
電界強度
クーロンの法則から、この場に配置された別の電荷に作用する特定の電荷の電場強度は、場のすべての点で同じではないことがわかります。任意の点の電場は、その点に置かれた単位正電荷に作用する力の大きさによって特徴付けることができます。
この値がわかれば、各電荷 Q に作用する力 F を決定できます。F = Q x E と書くことができます。ここで、F は、電場によって場の点に置かれた電荷 Q に作用する力、E は場の同じ点に置かれた単位正電荷に作用する力。場の特定の点で単位正電荷が受ける力に数値的に等しい量 E は、電場の強度と呼ばれます。