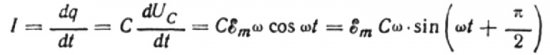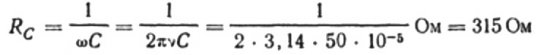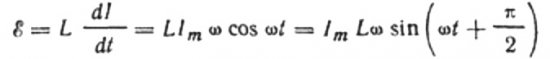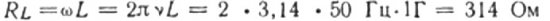交流回路における容量性抵抗と誘導性抵抗

DC 回路にコンデンサを含めると、定義上、誘電体は直流電流を通さないため、直流電流はプレート間の誘電体を通過できないため、抵抗は無限大であることがわかります。

コンデンサは直流回路を遮断します。しかし、同じコンデンサが交流回路に含まれている場合、そのコンデンサは完全に壊れているようには見えず、単に交互に充電されているだけであることがわかります。つまり、電荷が移動し、外部回路の電流は維持された。

この場合のマクスウェル理論に基づくと、コンデンサ内の交流伝導電流は、この場合にのみバイアス電流によって閉じられたままであると言えます。これは、AC 回路内のコンデンサが一種の有限値抵抗として機能することを意味します。この抵抗はと呼ばれます 容量性.

導体を流れる交流の量は、その導体の形状とその周囲の媒体の磁気特性に依存することが、実践的に長い間証明されてきました。まっすぐな線が最も電流が大きくなり、同じ線を多く巻いてコイルに巻くと電流は小さくなります。

そして、同じコイルに強磁性コアが導入されると、電流はさらに減少します。したがって、ワイヤはオーム (アクティブ) 抵抗だけでなく、ワイヤのインダクタンスに応じて追加の抵抗も伴って交流を供給します。 誘導的な.

その物理的意味は、特定のインダクタンスの導体に電流が変化すると、その導体に自己誘導の EMF が発生し、電流の変化が妨げられる、つまり電流が減少するということです。これは、ワイヤの抵抗が増加することと同じです。

交流回路の静電容量

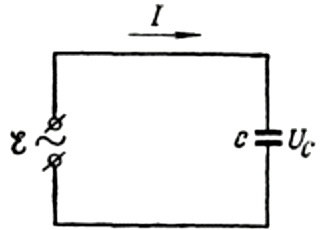
まず、容量抵抗について詳しく説明します。静電容量 C のコンデンサが正弦波交流電源に接続されていると仮定すると、この電源の EMF は次の式で表されます。

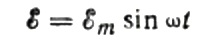
接続ワイヤ間の電圧降下は通常非常に小さく、必要に応じて個別に考慮できるため、無視します。ここで、コンデンサのプレート間の電圧が AC 電源電圧に等しいと仮定します。それから：

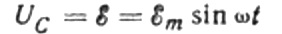
いかなる瞬間においても、コンデンサの電荷はその静電容量とプレート間の電圧に依存します。次に、上記の既知の電源を考慮すると、電源電圧によってコンデンサ プレートの電荷を求めるための式が得られます。

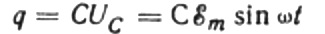
微小時間 dt の間、コンデンサの電荷が dq だけ変化すると、電源からコンデンサまでワイヤを通って流れる電流 I は次のようになります。

現在の振幅の値は次のようになります。

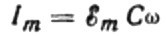
電流の最終的な式は次のようになります。

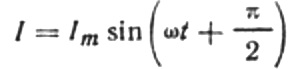
電流振幅の式を次のように書き換えてみましょう。

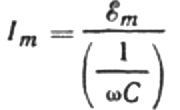
この比はオームの法則であり、角周波数と静電容量の積の逆数が抵抗の役割を果たし、実際には正弦波交流回路のコンデンサの静電容量を求めるための式です。

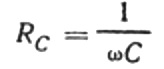
これは、容量性抵抗が電流の角周波数とコンデンサの静電容量に反比例することを意味します。この依存性の物理的な意味を理解するのは簡単です。

AC 回路のコンデンサの静電容量が大きくなり、回路内の電流の方向が頻繁に変化するほど、最終的にはコンデンサを AC 電源に接続するワイヤの断面を単位時間あたりに通過する総電荷の量が多くなります。これは、電流が静電容量と角周波数の積に比例することを意味します。

たとえば、周波数 50 Hz の正弦波交流回路の電気容量 10 マイクロファラッドのコンデンサの静電容量を計算してみましょう。

周波数が 5000 Hz の場合、同じコンデンサは約 3 オームの抵抗を示します。

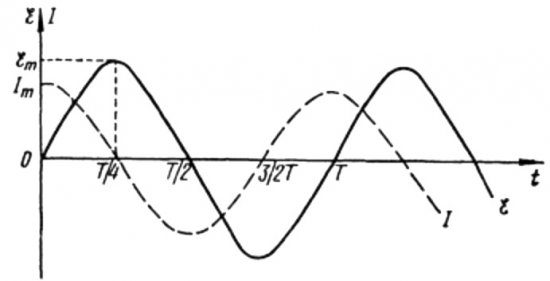
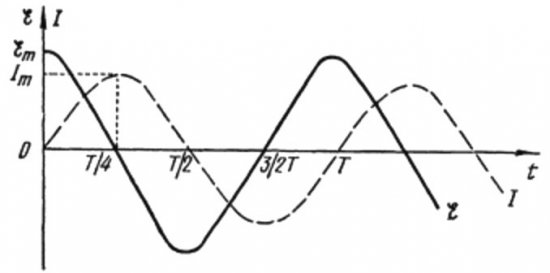
上記の式から、コンデンサを使用した交流回路の電流と電圧は常に異なる位相で変化することがわかります。電流位相は電圧位相より pi / 2 (90 度) 進みます。これは、最大電流が常に最大電圧よりも 4 分の 1 周期早く存在することを意味します。したがって、容量性抵抗の両端では、電流は電圧よりも期間の 4 分の 1、つまり位相が 90 度進みます。

この現象の物理的意味を説明しましょう。最初の瞬間、コンデンサは完全に放電されているため、コンデンサに印加されたわずかな電圧によってすでにコンデンサのプレート上の電荷が移動し、電流が生成されます。

コンデンサが充電されると、そのプレート間の電圧が増加し、それ以上の電荷の流れが妨げられるため、プレートに印加される電圧がさらに増加し​​ても、回路内の電流は減少します。

これは、最初の瞬間に電流が最大であった場合、4分の1周期後に電圧が最大に達すると、電流が完全に停止することを意味します。

期間の開始時に電流は最大、電圧は最小となり増加し始めますが、期間の 4 分の 1 が経過すると電圧は最大に達しますが、この時点では電流はすでにゼロに低下しています。したがって、電圧が周期の 4 分の 1 だけ進んでいることがわかります。

交流誘導抵抗

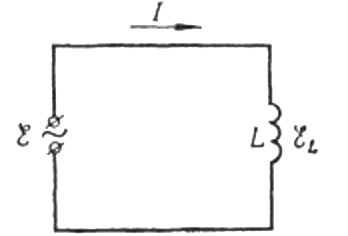
さて、誘導抵抗の話に戻ります。交流正弦波電流がインダクタンスのコイルを流れると仮定します。これは次のように表現できます。

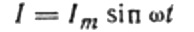
電流はコイルに印加される交流電圧によるものです。これは、自己誘導の EMF がコイルに現れることを意味し、次のように表されます。

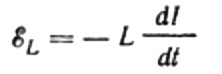
繰り返しますが、EMF 源をコイルに接続するワイヤでの電圧降下は無視します。オーム抵抗は非常に低いです。

任意の瞬間にコイルに印加される交流電圧が、その大きさに等しいが方向が逆である自己誘導の発生する EMF によって完全にバランスが取れているとします。

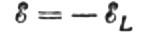
その場合、私たちには次のように書く権利があります。

コイルに印加される電圧の振幅は次のようになります。

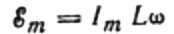
我々が得る：

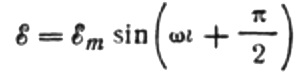
最大電流を次のように表します。

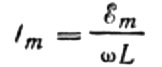
この式は本質的にオームの法則です。ここでは、インダクタンスと角周波数の積に等しい量が抵抗の役割を果たし、インダクタの誘導抵抗にほかなりません。

したがって、誘導抵抗はコイルのインダクタンスとそのコイルを流れる交流の角周波数に比例します。

これは、誘導抵抗が電源電圧に対する自己誘導起電力の影響によるものであるためです。自己誘導起電力は電流を減少させる傾向があるため、回路内に抵抗が生じます。知られているように、自己誘導起電力の大きさは、コイルのインダクタンスとコイルを流れる電流の変化率に比例します。

たとえば、電流周波数 50 Hz の回路に含まれる、インダクタンス 1 H のコイルの誘導抵抗を計算してみましょう。

ボールの周波数が 5000 Hz の場合、同じコイルの抵抗は約 31,400 オームになります。コイル ワイヤのオーム抵抗は通常数オームであることを思い出してください。

上記の式から、コイルを流れる電流とコイル内の電圧の変化は異なる位相で発生し、電流の位相は常に pi / 2 の電圧の位相より小さいことが明らかです。最大電流は、最大応力の開始から 4 分の 1 周期遅れて発生します。

誘導抵抗では、自己誘導起電力の制動効果により電流が電圧より 90 度遅れ、電流の変化 (増加と減少の両方) が妨げられるため、後でコイルを含む回路で最大電流が観察されます。最大電圧を超えています。

コイルとコンデンサの複合動作

コイルとコンデンサを交流回路に直列に接続すると、コイル電圧はコンデンサ電圧よりも時間的に半周期、つまり位相が 180 度進みます。

容量性抵抗と誘導性抵抗はこう呼ばれます 反応物… リアクティブ抵抗では、アクティブ抵抗のようにエネルギーが消費されません。コンデンサに蓄えられたエネルギーは、コンデンサ内の電場が消えると定期的に電源に戻されます。

これはコイルでも同じです。コイルの磁場が電流によって生成されると、コイル内のエネルギーは周期の 4 分の 1 の間に蓄積され、周期の次の 4 分の 1 の間に磁場が発生源に戻ります。この記事では、これらの規制が厳密に遵守されている正弦波交流について説明しました。

AC正弦波回路では、コア付きインダクタは次のように呼ばれます。 窒息する伝統的に電流制限に使用されます。加減抵抗器に対する利点は、エネルギーが熱として大量に放散されないことです。