電気工学およびエレクトロニクスにおける振動プロセス、振動の種類
振動プロセス — さまざまな程度の再現性を持つプロセス。すべての振動プロセスは、周期的と非周期的の 2 つのクラスに分類されます。理論的には、ほぼ周期的な振動である中間クラスも使用されます。
振動プロセスは周期的と呼ばれ、このプロセスを特徴付ける値は、特定の期間 T 後のいつでも同じ値になります。
振動過程の数学的表現である関数 f (t) は、条件 f (t + T) = f (t) を満たす場合、周期 T の周期的と呼ばれます。
周期的な振動過程の中で、主な役割は調和振動または正弦振動であり、正弦または余弦の法則に従って時間の経過に伴う物理量の変化が発生します。彼らの全体的な記録は次のとおりです。
y = f (t) = aCos ((2π / T) t — φ)、
ここで、a - 振動の振幅、φ は振動の位相、1 /T = f - 周波数、2πf = ω - 周期的または円形振動の周波数です。
正弦波振動の応用とその特性:
周期的な振動の読み取り値に対応するほぼ周期的な関数は、次の条件によって定義されます。
| f · (t + τ) — f (t) | <= ε ここで、ε — 各値 T に値を割り当てます。
この場合の量 τ をほぼ周期と呼びます。値 ε が時間 T における f (t) の平均値と比較して非常に小さい場合、準周期関数は周期関数に近くなります。
非周期振動は周期振動よりもはるかに多様です。しかし、オートメーションではほとんどの場合、正弦波振動の減衰または増加に対応する必要があります。
減衰正弦波の法則に従った振動、または減衰調和振動とも呼ばれる振動は、一般的な形式で表すことができます。
x = Ae-δTcos・(ω + φ)、
ここで、t は時間、A と φ は任意の定数です。増加する調和振動の法則の一般的な表記法は、減衰係数 δ[1 秒] の符号が異なるだけです。
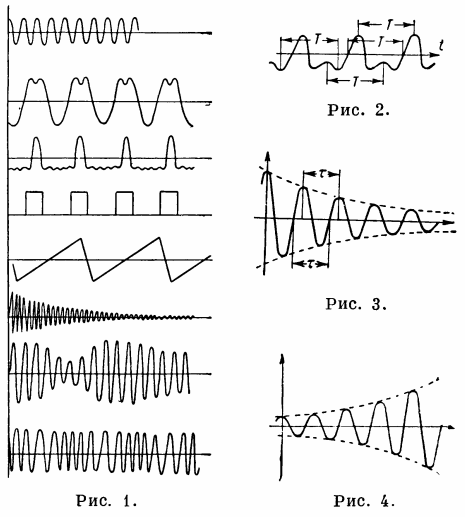
イチジク。 1 - 振動プロセス、図。 2. — 周期的なプロセス、図。 3. — 減衰調和振動、図。 4. — 高調波振動の増加。
振動プロセスの応用例は、最も単純な振動回路です。
発振回路 (電気回路) — 回路自体のパラメータによって決定される周波数で電気発振が発生する受動的な電気回路。
最も単純な発振回路は、キャパシタンス C とインダクタンス L で構成されます。外部の影響がない場合、周波数 εО = 1/2π√LC で発振が減衰します。
振動の振幅は eg-δT で減少します。ここで、δ は減衰係数です。 δ> = e0 の場合、回路内の減衰振動は非周期的になります。
エレクトロニクスでは、発振回路の品質は品質係数によって決まります: Q = nf/δ... 外部から周期的な力が発振回路に作用すると、強制発振が発生します。外部影響の周波数が eo (共振) に近い場合、強制発振の振幅は高 Q 回路で大幅に増加します。発振回路は共振増幅器の主要部品の一つであり、 発電機 およびその他の電子機器。
このトピックについては、以下も参照してください。 電圧共振と電流共振の応用
