非正弦波電流を使用する電気回路
非正弦波電流とその分解
 電気回路では、次の 2 つの理由で非正弦波電流が発生することがあります。
電気回路では、次の 2 つの理由で非正弦波電流が発生することがあります。
-
電気回路自体は線形ですが、非正弦波電圧が回路に作用します。
-
回路に作用する電圧は正弦波ですが、電気回路には非線形要素が含まれています。
両方の理由が考えられます。この章では、最初のポイントの回路のみを扱います。この場合、非正弦波電圧は周期的であると考えられます。
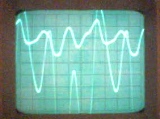
周期パルスの発生器は、無線工学、オートメーション、テレメカニクスのさまざまなデバイスで使用されます。パルスの形状は、鋸歯状、階段状、長方形などさまざまです (図 1)。
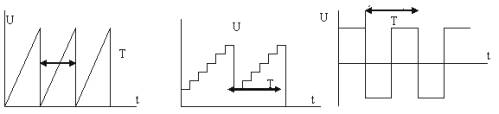
図 1. パルス形状
周期的だが非正弦波の電圧下で線形電気回路で発生する現象は、電圧曲線を三角フーリエ級数で展開すると最も簡単に研究できます。
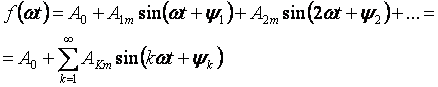
系列 A0 の最初の項は定数成分またはゼロ次高調波と呼ばれ、系列の 2 番目の項は定数成分またはゼロ次高調波と呼ばれます。
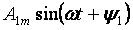
— 基本波または第 1 高調波、およびフォームの他のすべてのメンバー
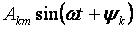
k> 1 の場合は高調波と呼ばれます。
式 (3.1) で和の正弦を開くと、級数を別の形式で書くことができます。
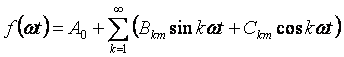 関数が横軸に関して対称である場合、その系列には定数成分が含まれません。関数が縦軸に関して対称である場合、系列には正弦が含まれません。この関数は原点に関して対称であり、コサインは含まれません。
関数が横軸に関して対称である場合、その系列には定数成分が含まれません。関数が縦軸に関して対称である場合、系列には正弦が含まれません。この関数は原点に関して対称であり、コサインは含まれません。
級数展開の例をいくつか表に示します。これらは参考文献からも入手できます。
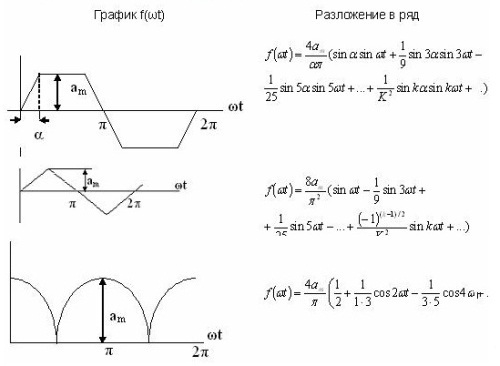
表 1. フーリエ級数展開
非正弦波電流回路の計算
回路はモデルに従って高調波ごとに計算されます。回路は、回路に作用する電圧に含まれる高調波の数だけ計算されます。この場合、多くの特性を考慮する必要があります。
高調波数が増加すると、誘導素子の抵抗が増加することに注意してください。
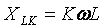
逆に、容量性要素は減少します。

また、電流の一定成分はコンデンサを通過せず、インダクタンスはコンデンサに対する抵抗ではないことも考慮する必要があります。
さらに、基本高調波だけでなく、高調波でも共振現象が発生する可能性があることを忘れてはなりません。
ベクトル図 高調波ごとに個別にプロットできます。
重ね合わせの原理によれば、各ブランチの電流は個々の項 (ゼロ、基本波、高調波) の合計で構成されます。
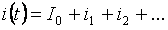
合計分岐電流の実効値は、個々の高調波電流の平均値によって決定できます。
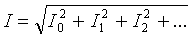
非正弦波電流の有効電力は、個々の高調波の有効電力の合計に等しくなります。
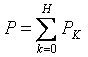
以下は、非正弦波電流回路を計算するための一般的な例です。すべての電流、電圧、抵抗には 2 つのインデックスがあります。最初の桁は枝番号を意味し、2 番目の桁は高調波番号を意味します。入力電圧:
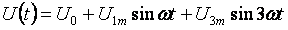
- 永久コンポーネント
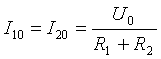
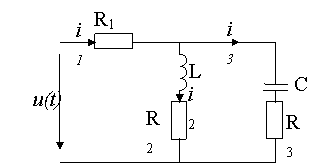
図 2. 電気回路図
- 主高調波:
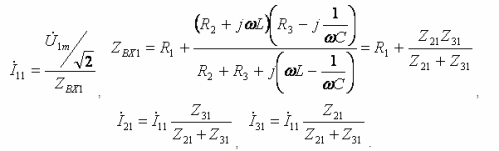
- 第三高調波:
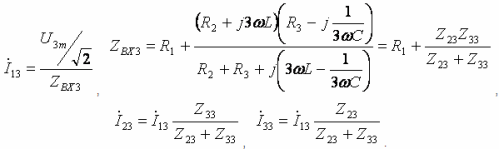
こちらもお読みください: 最も一般的な AC から DC への整流方式
