エネルギー保存の法則
現代物理学は、さまざまな物体や粒子の運動やさまざまな相互配置に関連する多くの種類のエネルギーを知っています。たとえば、移動する物体は、その速度の 2 乗に比例する運動エネルギーを持っています。このエネルギーは、体の速度が増減すると変化する可能性があります。地面から持ち上げられた物体には、物体の高さが 3 回変化する重力位置エネルギーがあります。
互いにある程度の距離にある静止電荷は、クーロンの法則に従って、電荷は (符号が異なる場合に) 引き合うか、または の 2 乗に反比例する力で反発するという事実に従って、静電的な位置エネルギーを持ちます。それらの間の距離。
運動エネルギーと位置エネルギーは、分子、原子、粒子、その構成要素である電子、陽子、中性子などによって所有されています。機械的仕事の形、電流の流れ、熱の伝達、物体の内部状態の変化、電磁波の伝播など。
100 年以上前、エネルギーは無から消滅したり、無から発生したりすることはないという基本的な物理法則が確立されました。彼女はあるタイプから別のタイプにのみ変更できます…。この法則をエネルギー保存則といいます。
A. アインシュタインの著作では、この法則が大幅に発展しました。アインシュタインは、エネルギーと質量の交換可能性を確立し、それによってエネルギー保存則の解釈を拡大しました。これは現在、エネルギーと質量の保存則として一般的に言われています。
アインシュタインの理論によれば、物体のエネルギー dE の変化は、公式 dE =dmc2 によって質量 dm の変化に関連付けられます。ここで、c は 3 x 108 Miss に等しい真空中の光の速度です。
特に、この式から、あるプロセスの結果として、そのプロセスに関与するすべての物体の質量が 1 g 減少した場合、そのエネルギーは 9×1013 J に等しく、これは 3000 トンのエネルギーに相当します。標準燃料。
これらの比率は核変換の解析において最も重要です。ほとんどの巨視的な過程では、質量の変化は無視でき、エネルギー保存則のみが語られます。
いくつかの具体例でエネルギーの変化をたどってみましょう。旋盤で部品を製造するために必要なエネルギー変換のチェーン全体を考えてみましょう (図 1)。ある量の化石燃料が完全燃焼して、その量を100%とする初期エネルギー1が得られるとします。したがって、この例では、初期エネルギーの 100% が、高温 (約 2000 K) の燃料燃焼生成物に含まれています。
発電所のボイラー内での燃焼生成物は冷却されると、その内部エネルギーを熱の形で水と水蒸気に放出します。しかし、技術的および経済的理由により、燃焼生成物を周囲温度まで冷却することはできません。それらは管を通して約 400 K の温度で大気中に放出され、元のエネルギーの一部が奪われます。したがって、初期エネルギーの 95% のみが水蒸気の内部エネルギーに変換されます。
結果として生じる水蒸気は蒸気タービンに入り、そこでその内部エネルギーが最初に部分的に蒸気ストリングの運動エネルギーに変換され、その後機械エネルギーとしてタービンローターに伝達されます。
蒸気エネルギーの一部のみが機械エネルギーに変換できます。残りは復水器で蒸気が凝縮する際に冷却水に与えられます。この例では、タービン ローターに伝達されるエネルギーは約 38% であると仮定しました。これは、現代の発電所の状況にほぼ対応しています。
いわゆる機械エネルギーを電気エネルギーに変換するとき、発電機の回転子および固定子巻線のジュール損失により、エネルギーの約 2% が失われます。その結果、初期エネルギーの約 36% がグリッドに送られることになります。
電気モーターは、供給された電気エネルギーの一部のみを機械エネルギーに変換して旋盤を回転させます。この例では、モーター巻線のジュール熱とベアリングの摩擦熱の形でエネルギーの約 9% が周囲の大気中に放出されます。
したがって、初期エネルギーの 27% のみが機械の作動器官に供給されます。しかし、エネルギー事故はこれで終わりではありません。部品の加工中のエネルギーのほとんどは摩擦に費やされ、部品を冷却する液体によって熱の形で除去されることがわかりました。理論的には、元の部品の目的の部分を取得するには、初期エネルギーのごく一部 (この例では 2% と想定) だけで十分です。
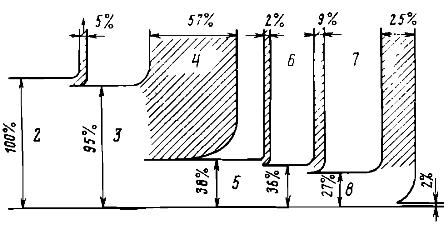
米。 1. 旋盤でワークを加工する際のエネルギー変換の図: 1 - 排気ガスによるエネルギー損失、2 - 燃焼生成物の内部エネルギー、3 - 作動流体の内部エネルギー - 水蒸気、4 - 冷却から放出される熱タービン凝縮器内の水、5 - タービン発電機のローターの機械エネルギー、6 - 発電機の損失、7 - 機械の電気駆動における廃棄物、8 - 機械の回転の機械エネルギー、9 - 摩擦仕事は熱に変換され、液体から分離され、冷却部品、10 — 加工後の部品とチップの内部エネルギーが増加します...
検討中の例がかなり典型的であると考えられる場合、この例から少なくとも 3 つの非常に有用な結論を引き出すことができます。
まず、エネルギー変換の各段階で、エネルギーの一部が失われます。この記述は、エネルギー保存の法則に違反するものとして理解されるべきではありません。これは、対応する変換が実行されることで得られる有用な効果により失われます。変換後のエネルギーの総量は変わりません。
エネルギー変換と伝達のプロセスが特定の機械または装置で行われる場合、このデバイスの効率は通常、効率（効率）によって特徴付けられます...そのようなデバイスの図を図に示します。 2.
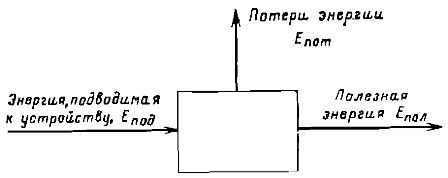
米。 2. エネルギーを変換するデバイスの効率を決定するためのスキーム。
図に示す表記を使用すると、効率は次のように定義できます。 Efficiency = Epol/Epod
この場合、エネルギー保存の法則に基づいて、Epod = Epol + Epot が存在することは明らかです。
したがって、効率は次のように書くこともできます: 効率 = 1 — (Epot / Epol)
図１に示す例に戻る。 1、ボイラーの効率は 95%、蒸気の内部エネルギーを機械的仕事に変換する効率は 40%、発電機の効率は 95%、効率は - 電気駆動装置であると言えます。機械の効率は 75%、ワークの実際の加工効率は約 7% です。
かつて、エネルギー変換の法則がまだ知られていなかったとき、人々の夢は、いわゆる永久機関、つまりエネルギーを消費せずに有用な仕事をする装置を作成することでした。このような架空のエンジンは、その存在がエネルギー保存の法則に違反するものであり、今日では第二種永久機関とは対照的に、第一種永久機関と呼ばれています。真剣に、最初の種類の永久機関を作成する可能性があります。
第二に、すべてのエネルギー損失は最終的に熱に変換され、熱は大気または自然の貯水池からの水に放出されます。
第三に、人々は、関連する有益な効果を得るために費やされる一次エネルギーのほんの一部しか最終的には使用しません。
これは、エネルギー輸送コストを見ると特に明らかです。摩擦力を考慮しない理想的な力学では、水平面内で荷重を移動させるのにエネルギーは必要ありません。
実際の状況では、車両が消費するすべてのエネルギーは、摩擦力と空気抵抗力を克服するために使用されます。つまり、最終的には、輸送で消費されるすべてのエネルギーが熱に変換されます。この点に関して、次の数字は興味深いもので、さまざまな種類の輸送手段を使用して 1 km の距離で 1 トンの貨物を移動する作業を特徴づけています。飛行機 — 7.6 kWh / (t-km)、自動車 — 0.51 kWh / ( t- km)、列車-0.12 kWh / (t-km)。
したがって、鉄道の 60 倍のエネルギー消費を犠牲にして、航空輸送でも同じ有益な効果を達成できます。もちろん、エネルギー消費量が多いと時間は大幅に節約されますが、同じ速度（車と電車）であっても、エネルギーコストは 4 倍異なります。
この例は、人々が快適性や速度などの他の目標を達成するために、エネルギー効率とのトレードオフを行うことが多いことを示唆しています。一般に、プロセス自体のエネルギー効率は、一般的な技術的および技術的な観点から、私たちにとってはほとんど関心がありません。プロセスの効率の経済的評価は重要です...しかし、一次エネルギー要素の価格が上昇するにつれて、技術的および経済的評価におけるエネルギー要素の重要性がますます高まっています。