単相変圧器の動作原理と装置
単相無負荷変圧器
電気工学における変圧器は、1 つの固定コイルからの交流電気エネルギーが、電気的に接続されていない別の固定コイルに伝達される電気装置と呼ばれます。
一方のコイルからもう一方のコイルにエネルギーを伝達するリンクは磁束です。磁束は 2 つのコイルと連動し、大きさと方向が常に変化します。
米。 1.
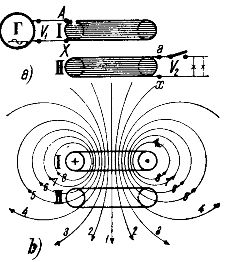
図では。図1aは、上下に同軸上に配置された2つの巻線/および//からなる最も単純な変圧器を示す。コイルへ/納品 交流電流 この巻線は一次巻線または一次巻線と呼ばれます。二次巻線または二次巻線と呼ばれる巻線 // を使用して、電気エネルギーの受信機を介して回路が接続されます。

変圧器の動作原理
トランスの動作は以下の通りです。一次巻線に電流が流れると、電流が発生します。 磁場、その力線は、それを作成した巻線だけでなく、部分的に二次巻線にも浸透します //。一次巻線によって形成される力線の分布の概略図を図に示します。 1b.
図からわかるように、すべての力線はコイル / の導体の周りで閉じていますが、図では一部の力線が閉じています。図1bに示すように、電線1、2、3、4もコイル//の電線の周囲で閉じられる。したがって、コイル // は、磁力線によってコイル // に磁気的に結合されます。
同軸配置のコイル / と // の磁気結合の度合いは、それらの間の距離に依存します。コイルが互いに離れるほど、コイル間の力線が少なくなるため、コイル間の磁気結合は小さくなります。コイル /コイルにくっつく //。
コイル / が通過するので、想定どおり、 単相交流つまり、ある法則、たとえば正弦の法則に従って時間の経過とともに変化する電流の場合、それによって生成される磁場も同じ法則に従って時間の経過とともに変化します。
たとえば、コイル内の電流 / が最大値を通過すると、コイルによって生成される磁束も最大値を通過します。コイル内の電流 / がゼロを通過して方向が変わると、磁束もゼロを通過して方向が変わります。
コイル // の電流を変化させると、コイル / と // の両方に磁束が侵入し、その値と方向が常に変化します。電磁誘導の基本法則によれば、コイルを貫く磁束が変化するたびに、コイル内に交流電流が誘導されます。 起電力…今回の場合、コイル // には自己誘導起電力が、コイル // には相互誘導起電力が発生します。
コイルの端が // 電気エネルギーの受信回路に接続されている場合 (図 1a を参照)、この回路に電流が発生します。したがって、受信機は電力を受け取ることになります。同時に、発電機から // 巻線によって回路に与えられるエネルギーとほぼ等しいエネルギーが // 巻線に送られます。このようにして、一方のコイルからの電気エネルギーは、第一コイルとは全く無関係な第二コイルの回路に電気的に(金属的に)伝達されることになりますが、この場合のエネルギー伝達手段は交流磁束のみとなります。
図に示されています。図1aに示すように、一次巻線/と二次巻線//との間に磁気結合がほとんどないため、変圧器は非常に不完全である。
2 つのコイルの磁気結合は、一般的に、2 つのコイルに結合する磁束と 1 つのコイルによって生成される磁束の比によって推定されます。
イチジク。図1bでは、コイル//の磁力線の一部だけがコイル//の周囲で閉じられていることがわかる。電力線の他の部分 (図 1b の線 6、7、8) は、コイル / の周囲でのみ閉じられています。これらの電力線は、最初のコイルから 2 番目のコイルへの電気エネルギーの伝達にはまったく関与せず、いわゆる漂遊磁界を形成します。
一次巻線と二次巻線の間の磁気結合を強化し、同時に磁束の通過時の磁気抵抗を減らすために、技術用変圧器の巻線は完全に閉じた鉄心に配置されます。
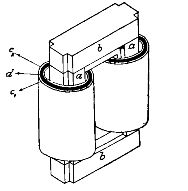
変圧器の実装の最初の例を図に概略的に示します。いわゆるロッドタイプの2単相変圧器。その一次コイル c1 と二次コイル c2 は鉄の棒 a ~ a 上に配置されており、端はヨークと呼ばれる鉄板 b ~ b で接続されています。このように、2本のロッドa、aと2つのヨークb、bは閉じた鉄のリングを形成し、その中を一次巻線と二次巻線で遮断された磁束が通過します。この鉄の輪を変圧器のコアといいます。
 米。 2.
米。 2.
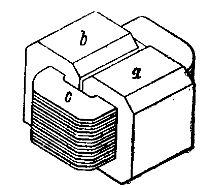
変圧器の第2の実施形態を図1に概略的に示す。 3 いわゆる装甲型の単相変圧器。この変圧器では、一次巻線と二次巻線 c が平坦巻線の列で構成され、2 つの鉄のリング a と b の 2 つのバーで形成されたコア上に配置されます。巻線を囲むリング a および b は、巻線のほぼ全体を装甲で覆っているため、説明されている変圧器は装甲と呼ばれます。コイル c 内を通過する磁束は 2 つの等しい部分に分割され、それぞれが独自の鉄のリングに囲まれます。
米。 3
変圧器に閉鉄磁気回路を使用することにより、漏れ電流が大幅に減少します。このような変圧器では、一次巻線と二次巻線に接続される磁束は互いにほぼ等しくなります。一次巻線と二次巻線に同じ磁束が貫通していると仮定すると、巻線の起電力の瞬時値の合計誘導衝撃に基づいて式を書くことができます。
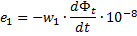
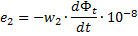
これらの式では、w1 と w2 - 一次巻線と二次巻線の巻数、dFt は時間要素 dt あたりの貫通巻線の磁束の変化の大きさです。したがって、磁束の変化率が存在します。 。最後の式から、次の関係が得られます。
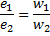
つまり一次巻線と二次巻線に表示される / および // 瞬間起電力は、コイルの巻き数と同じように相互に関係します。最後の結論は、起電力の瞬間値に関してだけでなく、その最大の実効値に関しても有効です。
一次巻線に誘導される起電力は、自己誘導の起電力として、同じ巻線に印加される電圧とほぼ完全に平衡します...E1とU1で起電力の実効値を示す場合一次巻線とそれに印加される電圧の関係を考慮すると、次のように書くことができます。
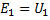
検討中のケースでは、二次巻線に誘導される起電力は、この巻線の両端間の電圧に等しくなります。
前のものと同様に、E2 と U2 を通じて二次巻線の起電力とその両端の電圧の実効値を指定する場合は、次のように書くことができます。
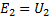
したがって、変圧器の一方の巻線に電圧を印加すると、もう一方のコイルの端に任意の電圧を得ることができます。必要なのは、これらのコイルの巻き数の適切な比率を取ることだけです。これが変圧器の主な特性です。
一次巻線の巻数と二次巻線の巻数の比をといいます。 変圧器の変圧比... 変換係数 kT を示します。
したがって、次のように書くことができます。
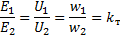
変圧器の変圧比が 1 より小さい変圧器は、二次巻線の電圧、いわゆる二次電圧が一次巻線の電圧、いわゆる一次電圧より大きいため、ステップアップ変圧器と呼ばれます。 。変圧比が 1 より大きい変圧器は、二次電圧が一次電圧より小さいため、降圧変圧器と呼ばれます。

負荷時の単相変圧器の動作
変圧器のアイドリング中、磁束は一次巻線電流によって、あるいは一次巻線の起磁力によって生成されます。トランスの磁気回路は鉄でできているため磁気抵抗が低く、一般に一次巻線の巻数が多いと考えられるため、トランスの無負荷電流は小さく、5-通常の 10%。
二次コイルをある程度の抵抗に近づけると、二次コイルに電流が発生すると、このコイルの起磁力も発生します。
レンツの法則によれば、二次コイルの起磁力は一次コイルの起磁力に逆らって作用します。
この場合の磁束は減少するはずですが、一次巻線に一定の電圧を印加すると磁束の減少はほとんどありません。
実際、トランスに負荷がかかったときに一次巻線に誘導される起電力は、印加電圧にほぼ等しくなります。この起電力は磁束に比例します。したがって、一次電圧の大きさが一定であれば、負荷時の起電力は変圧器の無負荷動作時とほぼ同じになるはずです。この状況により、いかなる負荷の下でも磁束がほぼ完全に一定になります。
 したがって、一次電圧が一定の値であれば、変圧器の磁束は負荷の変化によってほとんど変化せず、無負荷動作時の磁束と等しいとみなすことができます。
したがって、一次電圧が一定の値であれば、変圧器の磁束は負荷の変化によってほとんど変化せず、無負荷動作時の磁束と等しいとみなすことができます。
変圧器の磁束が負荷時にその値を維持できるのは、二次巻線に電流が現れると一次巻線の電流も増加し、一次巻線と二次巻線の起磁力またはアンペアターンの差が大きくなるからです。アイドリング中、巻線は起磁力またはアンペアターンにほぼ等しいままです...したがって、二次巻線に減磁起磁力またはアンペアターンが現れると、一次巻線の起磁力が自動的に増加します。
前述したように、トランス磁束を作るのに必要な起磁力は小さいため、二次起磁力が増加すると、ほぼ同じ大きさの一次起磁力も増加すると言えます。
したがって、次のように書くことができます。
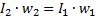
この等式から、変圧器の 2 番目の主な特性、つまり次の比率が得られます。
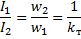
ここで、kt は変換係数です。
したがって、変圧器の一次巻線と二次巻線の電流の比は、変圧器の比で割ったものに等しくなります。
それで、 変圧器の主な特徴 関係がある
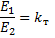
と
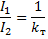
関係の左辺を互いに乗算し、右辺を互いに乗算すると、次のようになります。
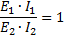
と
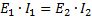
最後の等式は、変圧器の 3 番目の特性を与えます。これは、次のような言葉で表現できます。変圧器の 2 次巻線によって供給される電力 (ボルト アンペア) は、1 次巻線に供給される電力 (ボルト アンペア) とほぼ同じです。 。
巻線の銅と変圧器コアの鉄におけるエネルギー損失を無視すると、電源から変圧器の一次巻線に供給される電力はすべて二次巻線に伝達され、発信源は磁束です。
