交流とは何か、直流とどう違うのか

交流とは対照的に、 直流電流、大きさと方向の両方が常に変化しており、これらの変化は周期的に発生します。つまり、まったく同じ間隔で繰り返されます。

このような電流を回路に誘導するには、大きさと方向が周期的に変化する交流 EMF を生成する交流電源を使用します。このような電源はオルタネーターと呼ばれます。

図では。 1 は最も単純なデバイス図 (モデル) を示しています。 オルタネータ. 

銅線で作られた長方形のフレーム。軸に固定され、ベルトドライブを使用して現場で回転します。 磁石… フレームの端は銅のリングにはんだ付けされており、フレームとともに回転し、接触プレート (ブラシ) 上をスライドします。

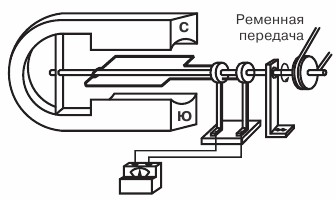
図 1. 最も単純なオルタネータの図

そのようなデバイスが実際に変動EMFの発生源であることを確認してみましょう。

磁石がその極の間に生じると仮定します。 均一な磁場つまり、場の各部分の磁力線の密度が同じであるものです。回転すると、フレームは a 面と b 面のそれぞれで磁力線を横切ります。 EMF 誘発. 

フレームの側面 c と側面 d は機能しません。これは、フレームが回転するときに、これらの側面が磁場の力線を横切らず、したがって EMF の生成に関与しないためです。

どの時点においても、サイド a で発生する EMF はサイド b で発生する EMF の方向が反対ですが、フレーム内では両方の EMF が作用し、総 EMF、つまりフレーム全体によって誘発される EMF に加算されます。

これは、EMF の方向を決定するために既知の右手の法則を使用すれば簡単に確認できます。

これを行うには、右手の手のひらを磁石の N 極に向けて置き、曲げた親指が EMF の方向を決定したいフレームのその側の移動方向と一致するようにします。次に、その中のEMFの方向が、伸ばした手の指によって示されます。

フレームのどのような位置であっても、側面 a と側面 b の EMF の方向を決定すると、それらは常に合計され、フレーム内の合計 EMF を形成します。同時に、フレームが回転するたびに、フレームの全EMFの方向が反対に変化します。これは、フレームの各作用面が1回転で磁石の異なる極の下を通過するためです。

フレームの側面が磁力線を横切る速度が変化すると、フレーム内に誘導される EMF の大きさも変化します。実際、フレームが垂直位置に近づき、フレームを通過する瞬間に、フレームの側面の力線を横切る速度が最も速くなり、最大の起電力がフレーム内に誘導されます。この瞬間、フレームが水平位置を通過するとき、フレームの側面は磁力線を横切ることなく磁力線に沿ってスライドするように見え、EMFは誘導されません。

したがって、フレームが均一に回転すると、EMF がその中に誘導され、大きさと方向の両方が周期的に変化します。

フレーム内で発生する EMF はデバイスで測定でき、外部回路に電流を生成するために使用できます。

使用する 電磁誘導現象、交流EMF、したがって交流を得ることができます。

産業用交流および 照明用 蒸気または水力タービンと内燃機関によって駆動される強力な発電機によって生成されます。

AC 電流と DC 電流のグラフ表示

グラフィカルな手法により、時間に応じて特定の変数が変化する過程を視覚化することができます。

時間の経過とともに変化する変数のプロットは、グラフの軸と呼ばれる 2 本の相互に垂直な線をプロットすることから始まります。次に、横軸には特定のスケールで時間間隔がプロットされ、縦軸には同じく特定のスケールでプロットされる量 (EMF、電圧または電流) の値がプロットされます。

図では。 2 グラフ化された直流電流と交流電流 ... この場合、電流値を遅延させます。通常正と呼ばれる一方向の電流値は、軸 O の交点から垂直に遅延されます。 、この点から下は反対方向、通常はマイナスと呼ばれます。

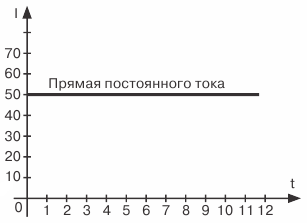
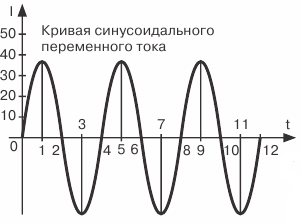図 2. DC と AC のグラフ表示

点 O 自体は、現在値 (垂直方向の下と上) と時間 (水平方向の右) の両方の原点として機能します。言い換えれば、この点は電流のゼロ値に対応し、そこから電流が将来どのように変化するかを追跡する予定のこの開始点に対応します。

図にプロットされた内容が正しいことを確認してみましょう。 2 と 50 mA DC 電流のプロット。

この電流は一定である、つまり時間の経過とともに大きさと方向が変わらないため、同じ電流値は異なる瞬間、つまり50 mAに対応します。したがって、ゼロに等しい瞬間、つまり電流を観測した最初の瞬間では、電流は 50 mA に等しくなります。縦軸に電流値 50 mA に等しい線分を上に描くと、グラフの最初の点が得られます。

時間軸上の点 1 に対応する次の瞬間にも同じことを行う必要があります。つまり、この点から垂直上方に同じく 50 mA に等しいセグメントを延期する必要があります。セグメントの終端がグラフの 2 番目の点を定義します。

その後のいくつかの時点に対して同様の構築を行うと、一連の点が得られ、その接続により直線が得られ、これは 50 mA の定電流値をグラフで表したものになります。

変数EMFのプロット

EMF の変数グラフの学習に進みましょう...図。図３では、磁場中で回転するフレームが上部に示されており、結果として生じる変数EMFのグラフ表示が以下に示されている。

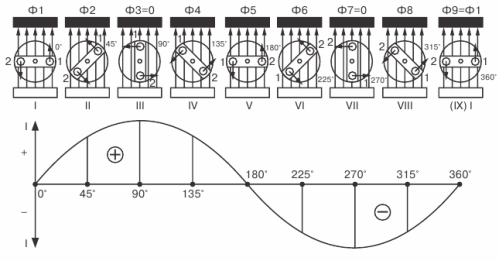図 3. 変数 EMF のプロット

フレームを時計回りに均一に回転させ始め、フレームの水平位置を初期瞬間として、EMF 変化の経過を追跡します。

この最初の瞬間では、フレームの側面が磁力線と交差していないため、EMF はゼロになります。グラフでは、t = 0 の瞬間に対応する EMF のゼロ値は点 1 で表されます。

フレームをさらに回転させると、EMF がフレーム内に現れ始め、フレームが垂直位置に達するまで増加します。グラフでは、この EMF の増加は、ピーク (ポイント 2) に達する滑らかな上昇曲線で表されます。

フレームが水平位置に近づくと、フレーム内の EMF は減少し、ゼロになります。グラフ上では、これは滑らかな下降曲線として描かれます。

したがって、フレームの半回転に相当する時間の間に、フレーム内の EMF はゼロから最大値まで増加し、再びゼロに減少することができました (ポイント 3)。

フレームをさらに回転させると、EMF が再びフレーム内に現れ、徐々に大きさが増加しますが、右手の法則を適用するとわかるように、その方向はすでに反対に変化しています。

グラフでは EMF の方向の変化が考慮されているため、EMF を表す曲線は時間軸と交差し、その軸の下に位置します。 EMF は、フレームが垂直位置になるまで再び増加します。

その後、EMF は減少し始め、フレームが完全に 1 回転した後に元の位置に戻ると、その値はゼロになります。これは、グラフ上では、EMF 曲線が逆方向にピークに達し (点 4)、時間軸と交わる (点 5) という事実によって表されます。

これで EMF 変更の 1 サイクルが完了しますが、フレームの回転を続けると、すぐに 2 番目のサイクルが開始され、最初のサイクルが正確に繰り返され、次に 3 番目、4 番目というように停止するまで続きます。回転フレーム。

したがって、フレームが回転するたびに、フレーム内で発生する EMF はその変化の完全なサイクルを完了します。

フレームが何らかの外部回路に接続されている場合、交流電流が回路を流れ、そのグラフは EMF グラフと同じように見えます。

結果として生じる波形は正弦波と呼ばれ、この法則に従って変化する電流、起電力、または電圧は正弦波と呼ばれます。

曲線自体は、正弦と呼ばれる可変三角関数量をグラフで表現したものであるため、正弦波と呼ばれます。

電流変化の正弦波的な性質は電気工学において最も一般的なものであるため、交流といえばほとんどの場合正弦波電流を意味します。

さまざまな交流（EMFと電圧）を比較するには、特定の電流を特徴付ける値があります。これらは AC パラメータと呼ばれます。

周期、振幅、周波数 - AC パラメータ

交流は月次周期と振幅という 2 つのパラメータによって特徴付けられ、これらを知ることで交流の種類を推定し、電流のグラフを作成できます。

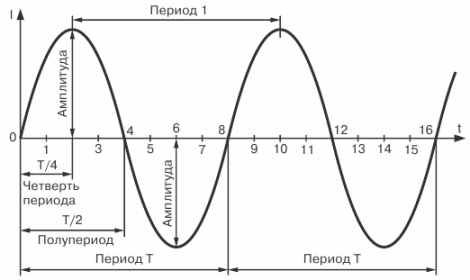
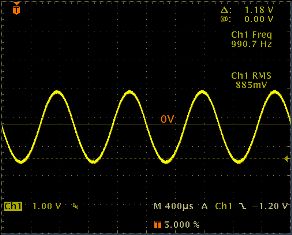
図 4. 正弦波電流曲線

電流変化の完全なサイクルが発生する期間を「期間」と呼びます。期間は文字 T で示され、秒単位で測定されます。

電流変化の完全なサイクルの半分が発生する期間を半サイクルと呼ぶため、電流 (EMF または電圧) の変化期間は 2 つの半周期で構成されます。同じ交流のすべての周期が互いに等しいことは明らかです。

グラフからわかるように、変化の 1 周期の間に、電流は最大値の 2 倍に達します。

交流電流 (EMF または電圧) の最大値は、その振幅またはピーク電流値と呼ばれます。

Im、Em、および Um は、電流、EMF、および電圧振幅の一般的な指定です。

まず最初に注目したのは、 ピーク電流ただし、グラフからわかるように、振幅よりも小さい中間値が無数に存在します。

選択された任意の瞬間に対応する交流電流 (EMF、電圧) の値は、その瞬間値と呼ばれます。

i、e、および u は、電流、起電力、電圧の瞬時値の一般に受け入れられている指定です。

グラフを使用すると、電流の瞬時値とピーク値を簡単に判断できます。これを行うには、関心のある時点に対応する水平軸上の任意の点から、現在の曲線との交点まで垂直線を描きます。結果として得られる垂直線のセグメントによって、特定の時間における電流の値、つまり瞬時値が決まります。

明らかに、グラフの開始点から時間 T / 2 後の電流の瞬時値はゼロになり、時間 T / 4 以降の振幅値はゼロになります。電流もピーク値に達します。しかし、3/4 T に等しい時間の後、すでに反対方向に進んでいます。

したがって、グラフは、回路内の電流が時間の経過とともにどのように変化するか、および電流の大きさと方向の両方の特定の 1 つの値だけが各瞬間に対応することを示しています。この場合、回路内のある時点での電流値は、その回路内の他の点でもまったく同じになります。

これは、AC 周波数の 1 秒間に電流が満たす完全な周期の数と呼ばれ、ラテン文字 f で表されます。

交流の周波数を決定するには、つまり、1 秒間に電流が何周期変化するかを調べるには、1 秒を 1 周期の時間で割る必要があります f = 1 / T。 周波数を知る交流の周期を決定できます: T = 1 / f

交流周波数 ヘルツと呼ばれる単位で測定されます。

周波数が 1 ヘルツに等しい交流がある場合、そのような電流の周期は 1 秒に等しくなります。逆に、電流の変化周期が 1 秒の場合、そのような電流の周波数は 1 ヘルツになります。

そこで、さまざまな AC 電流、EMF、電圧を区別し、必要に応じてそれらのグラフをプロットできるようにする AC パラメーター (周期、振幅、周波数) を定義しました。

さまざまな回路の交流に対する抵抗を決定するときは、交流を特徴付ける別の補助値、いわゆる角または角周波数。

周波数 f との関係を比 2 pif で表す円周周波数

この依存関係について説明しましょう。可変 EMF グラフをプロットすると、フレームが 1 回完全に回転すると、EMF 変化の完全なサイクルが生じることがわかりました。つまり、フレームが1回転する、つまり360°回転するのに、1周期に等しい時間、つまりT秒かかることになります。すると、1秒間にフレームが360°/T回転します。したがって、360°/Tはフレームが1秒間に回転する角度であり、フレームの回転速度を表し、通常角速度または円速度と呼ばれます。

しかし、周期 T は比率 f = 1 / T によって周波数 f に関係しているため、円周速度も周波数として表すことができ、360 ° f に等しくなります。

したがって、360°f であると結論付けました。ただし、計算に円周波を使用する便宜上、1 回転に対応する 360° の角度は 2pi ラジアンに等しい動径表現 (pi = 3.14) に置き換えられます。それで、最終的に 2pif を取得します。したがって、交流の角周波数を決定するには (起電力または電圧)、ヘルツ単位の周波数に定数 6.28 を掛ける必要があります。