電力線の抵抗、コンダクタンスと等価回路

電力線には、能動抵抗と誘導抵抗、能動抵抗と容量性コンダクタンスがその長さに沿って均等に分布しています。

送電ネットワークの実際の電気計算では、均一に分布した DC 線路を、有効 r と誘導 x の抵抗、有効 g と容量 b の導電率の組み合わせの定数に置き換えるのが通例です。この条件に対応する U 字型ラインの等価回路を図に示します。 1、a.

電圧が 35 kV、導電率が g および b 未満のローカル送電ネットワークを計算する場合は、直列接続された能動抵抗と誘導抵抗で構成されるより単純な等価回路を無視して使用できます (図 1、b)。

線形抵抗は次の式で求められます。

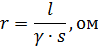
ここで、l はワイヤの長さ m です。 s はワイヤまたはケーブル コアの断面積、mmg γ は材料の特定の設計導電率、m / ohm-mm2 です。

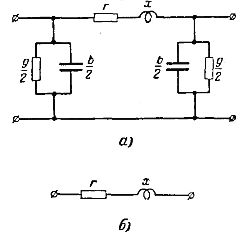
米。 1. 送電線代替スキーム: a — 地域送電網用。 b — ローカル送電ネットワーク用。

単芯線と多芯線の実際の断面積と多芯線を撚る際の長さの増加を考慮した、温度20℃における比導電率の平均計算値は53m/Ωです。・銅の場合は mm2、32 m/Ω ・アルミニウムの場合は mm2。

鋼線の有効抵抗は一定ではありません。ワイヤを流れる電流が増加すると、表面効果が増加するため、ワイヤのアクティブ抵抗が増加します。鋼線のアクティブ抵抗は、鋼線を流れる電流の値に応じて、実験的な曲線または表によって決定されます。

ライン誘導抵抗。三相電流線路がワイヤの再配置（転置）によって作成される場合、周波数 50 Hz で、線路長 1 km の相誘導抵抗は次の式で求めることができます。

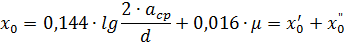
ここで、 asr はワイヤの軸間の幾何平均距離です。

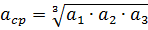
a1、a2、およびa3は、異なる位相の導体の軸間の距離です。dは、導体のGOSTテーブルに従って取得された導体の外径です。 μ は金属導体の比透磁率です。非鉄金属のワイヤの場合、μ = 1。 x'0 — 導体の外側の磁束による線路の外部誘導抵抗。 x «0 — 導体の内部に閉じられた磁束による線路の内部誘導抵抗。

線路長さ l km あたりの誘導抵抗

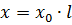
非鉄金属の導体を備えた架空線の誘導抵抗 x0 は、平均 0.33 ～ 0.42 オーム / km です。

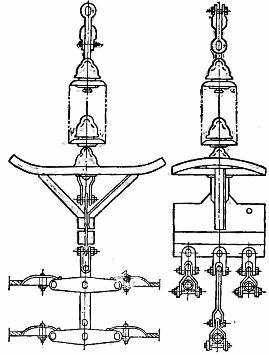
コロナ損失を低減するための 330 ～ 500 kV の電圧の送電線 (以下を参照) は、大きな直径の 1 つのコアではなく、相ごとに 2 つまたは 3 つの鋼アルミニウム導体を互いに短い距離に配置して実行されます。この場合、ラインの誘導抵抗は大幅に減少します。図では。図 2 は、500 kV 線路上の相の同様の実装を示しており、3 つの導体が辺 40 cm の正三角形の頂点に配置されており、相導体は断面内のいくつかの剛脈で固定されています。

相ごとに複数のワイヤを使用することは、ワイヤの直径を大きくすることと同じであり、これはラインの誘導抵抗の減少につながります。後者は、右側の第 2 項を n で割って、ワイヤの外径 d の代わりに、次の式で求められる等価直径 de を代入して、2 番目の式を使用して計算できます。

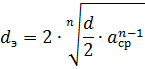
ここで、n — 線路の 1 つの相の導体の数。 acp — 1 つの相の導体間の幾何平均距離。

1 相あたり 2 本のワイヤの場合、ラインの誘導抵抗は約 15 ～ 20% 減少し、3 本のワイヤの場合 - 25 ～ 30% 減少します。

相導体の総断面積は必要な設計断面積に等しく、後者はとにかく 2 つまたは 3 つの導体に分割されるため、このような線路は従来から分割導体線路と呼ばれています。

鋼線の x0 値ははるかに大きくなります。 透磁率 が複数になり、2 番目の式の第 2 項が決定的になります。つまり、内部誘導抵抗 x «0 になります。

米。 2. 500 平方メートルの単相 3 分割ワイヤー吊り下げガーランド。

鋼の透磁率はワイヤを流れる電流の値に依存するため、鋼ワイヤから x «0 を決定することは非常に困難です。したがって、実際の計算では、実験的に得られた曲線や表から鋼線のx»0を求めます。

3 芯ケーブルの誘導抵抗は、次の平均値に基づいて求めることができます。

• 3 線ケーブルの場合 35 kV — 0.12 オーム / km

• 3 線ケーブルの場合 3-10 kv-0.07-0.03 オーム / km

• 3 線ケーブルの場合、最大 1 kV-0.06 ～ 0.07 オーム/km

アクティブな導電線は、誘電体における有効電力の損失によって定義されます。

どの電圧の架空線でも、大気汚染の激しい地域であってもがいしによる損失は小さいため考慮していません。

電圧 110 kV 以上の架空線では、特定の条件下で、電線周囲の空気の激しいイオン化により、紫色の輝きと特有のパチパチ音を伴うコロナが電線上に発生します。ワイヤークラウンは雨天時に特に威力を発揮します。コロナによる電力損失を減らす最も抜本的な手段は、導体の直径を大きくすることです。直径が大きくなると、電界の強度が低下し、したがって導体近くの空気のイオン化が減少するためです。

110 kV 送電線の場合、コロナ条件からの導体の直径は少なくとも 10 ～ 11 mm (導体 AC-50 および M-70)、154 kV 送電線の場合 - 少なくとも 14 mm (導体 AC-95) である必要があります。 220 kV ラインの場合 — 22 mm 以上 (導体 AC -240)。

指定された大きな導体直径の 110 ～ 220 kV 架空線の導体におけるコロナによる有効電力損失はわずかであるため (線路長 1 km あたり数十キロワット)、計算では考慮されません。

330 および 500 kV の送電線では、各相に 2 つまたは 3 つの導体が使用されます。これは、前述したように、導体の直径が増加することに相当し、その結果、導体付近の電界の強度が大幅に増加します。減少しており、導体はわずかに腐食しています。

35 kV 以下のケーブル線では、誘電体での電力損失は小さいため、考慮されていません。電圧が 110 kV 以上のケーブル線では、誘電損失は長さ 1 km あたり数キロワットに達します。

導体間および導体とアース間の静電容量による線路の容量性伝導。

三相架空線の容量性コンダクタンスは、実際の計算に十分な精度で次の式で求めることができます。

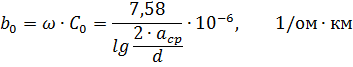
ここで、C0 はラインの動作容量です。 ω — 交流の角周波数。 acp と d — 上記を参照してください。

この場合、土壌の導電率や地上に戻る電流の深さは考慮せず、線路に沿って導体を再配置すると仮定する。

ケーブルの場合、使用容量は工場出荷時のデータに従って決定されます。

線伝導率 l km

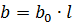
ライン内に静電容量が存在すると、容量性電流が流れます。容量性電流は、対応する相電圧より 90°進んでいます。

一定の容量性電流が長さに沿って均一に分布している実際の線路では、線路にかかる電圧の大きさが一定ではないため、容量性電流は線路の長さに沿って均一ではありません。

直流電圧を受ける線路の始点の容量性電流

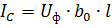
ここで、Uph は線相電圧です。

容量性線路電力（線路によって生成される電力）

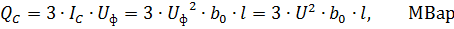
ここで、U は相間電圧 sq です。

3 番目の式から、線路の容量性導電率は導体間の距離と導体の直径にはほとんど依存しないことがわかります。線路によって生成される電力は、線路電圧に大きく依存します。 35 kV 以下の架空線の場合、この値は非常に小さくなります。長さ 100 km の 110 kV 送電線の場合、Qc ≈ 3 Mvar です。長さ 100 km の 220 kV 送電線の場合、Qc ≈ 13 Mvar。分割線を使用すると線容量が増加します。

ケーブル ネットワークの容量電流は、20 kV 以上の電圧でのみ考慮されます。