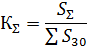電気負荷を計算するための係数

電気ネットワークを計算するタスクは、値を正しく推定することです 電気負荷 そして、それぞれ、以下に関して標準化された条件が満たされるワイヤ、ケーブル、バスバーの可能な最小断面の選択です。

1.電熱線、

2. 経済的な電流密度、

3. ネットワークの個々のセクションの電気的保護、

4. ネットワーク内の電圧損失、

5. ネットワークの機械的強度。

ワイヤの断面を選択するための設計荷重は次のとおりです。

1. 30 分最大 I30 - 加熱断面積の選択用、

2. 平均スイッチング負荷 Icm — 経済的な電流密度の断面積を選択するため、

3. ピーク電流 — ヒューズの選択と過電流サーキットブレーカーの電流設定、および電圧損失の計算に使用されます。この計算は通常、個々の高出力のかご型モーターやトロリーバスを始動するときの電源ネットワークでの電圧損失を決定することに要約されます。

配電ネットワークの断面を選択するときは、受電器の実際の負荷率に関係なく、受電器を最大容量で使用する可能性を常に考慮する必要があるため、受電器の定格電流は次のように考慮する必要があります。定格電流。例外は、加熱用ではなく過負荷トルク用に選択された電気モーターへの配線にのみ許可されます。

したがって、流通ネットワークの場合、決済自体は行われません。

供給ネットワークの推定電流を決定するには、多数のエネルギー消費者と、通常は異なる動作モードの合計最大負荷または平均負荷を見つける必要があります。その結果、電力ネットワークを計算するプロセスは比較的複雑になり、次の 3 つの主要な連続操作に分割されます。

1. 計算スキームを作成する、

2. ネットワークの個々のセクションにおける合計最大負荷またはその平均値の決定、

3. セクションの選択。

設計スキームは、電気エネルギーの分配を検討する際に概説された電源コンセプトを発展させたもので、接続された負荷、ネットワークの個々のセクションの長さ、選択された敷設のタイプと方法に関する必要なデータをすべて含める必要があります。 。

最も重要な操作であるネットワークの個々のセクションの電気負荷の決定は、ほとんどの場合、経験式の使用に基づいています。これらの式に含まれる係数は、電気エネルギーの消費者の動作モードに最も大きく依存し、後者の正しい評価は非常に重要ですが、常に正確であるとは限りません。

同時に、係数の決定の不正確さ、およびそれに伴う負荷の決定が、ネットワークの帯域幅の不足や、設備全体の価格の不当な上昇につながる可能性があります。

電力網の電気負荷を決定する方法論に進む前に、計算式に含まれる係数が安定していないことに注意する必要があります。継続的な技術進歩と自動化の発展により、これらの要素は定期的に見直す必要があります。

なお、計算式そのものや計算式に含まれる係数はある程度近似的なものであるため、計算結果は利息額の順位を決定するに過ぎないことを留意する必要がある。避けるべきです。

電気負荷を決定するための計算式に含まれる値と係数

設置容量 Ru は次のことを意味します。

1. 連続運転の電気モーターの場合 — カタログ (パスポート) の公称出力 (キロワット単位)、シャフト モーターによって開発されたもの:

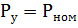
2. 断続動作の電気モーターの場合 — 公称電力が連続動作に減少します。つまり、対 PV = 100%:

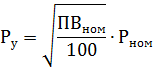
ここで、PVN0M はカタログ データに基づく定格デューティ サイクル (パーセント)、Pnom は PVN0M での定格電力、

3. 電気炉変圧器の場合:

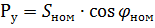
ここで、СХ0Мはカタログデータによる変圧器の定格電力、kVA、cosφnomは定格電力での電気炉の運転の力率特性、

4. 溶接機および装置の変圧器用 — 条件付き電力が連続運転に削減されます。対 PV = 100%:

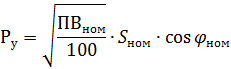
ここで、Snom は変圧器のデューティ サイクル定格 (キロボルト アンペア) です。

接続された電源の下で、電気モーターの Ppr は、公称負荷と電圧でネットワークからモーターによって消費される電力として理解されます。

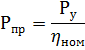
ここで、ηnom は相対単位で表したモーター定格電力です。

最も負荷の高いシフトの平均有効負荷 Rav.cm と同じ平均無効負荷 Qcp, cm は、最大負荷シフト中に消費される電力量 (それぞれ WCM と VCM) をシフト期間時間 Tcm で割った係数です。

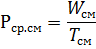
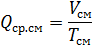
平均年間有効負荷 Rav.g と同じ無効負荷 Qcp.g は、年間電力消費量 (それぞれ Wg と Vg) を年間稼働時間 (Tg) で割った係数です。

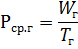
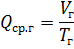
最大負荷の下では、Rmax は特定の時間間隔の最大平均負荷として理解されます。

PUEに準拠、加熱ネットワークと変圧器の計算では、この時間間隔は 0.5 時間に等しく設定されます。つまり、最大負荷は 30 分であると想定されます。

30 分間の最大負荷を区別します: アクティブ P30、kW、リアクティブ Q30、kvar、フル S30、kVA、および電流 I30、a。

ピーク電流 Ipeak は、特定の電気エネルギー消費者または電気消費者のグループにとって可能な瞬間最大電流です。

KI の変化に対する利用率の下で、最大積載変位に対する平均有効荷重と設置電力の比率を理解します。

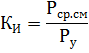
したがって、年間利用率は、設置容量に対する平均年間有効負荷の比率になります。

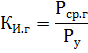
最大係数 Km は、最大負荷シフトの平均負荷に対するアクティブな 30 分ごとの最大負荷の比率として理解されます。

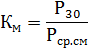
最大係数の逆数は、Kzap グラフの充填係数です。

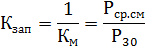
需要係数 Ks は、設置容量に対するアクティブな 30 分の最大負荷の比率です。

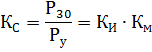
包含係数のもとでは、Kv は、シフトの継続時間に対する、シフトの反復された短期および長期動作モードの受信機の稼働時間の比率として理解されます。

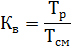
スイッチング中に連続動作するように設計された電気受信機の場合、スイッチング係数は実質的に 1 に等しくなります。

有効電力の負荷率 K3 は、所定の時間 Pt における受電器の負荷と設置電力の比率です。

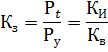
設置電力がシャフト電力として理解される電気モーターの場合、Ki、Kv、K3 を設置電力ではなく、ネットワークに接続された電源に帰する方がより正確です。

ただし、計算を簡素化するため、また電気モーターの負荷に関係する効率を考慮するのが難しいため、これらの要素は設置電力も参照することをお勧めします。したがって、1 に等しい需要率 (Kc = 1) は、電動機の実際の負荷の η% に相当します。

最大負荷の組み合わせ係数 KΣ は、電力消費者のいくつかのグループの 30 分あたりの最大負荷の組み合わせと、個々のグループの 30 分あたりの最大負荷の合計との比です。

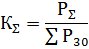
実用上許容される近似では、次のように仮定できます。

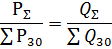
そしてその結果として