並列励磁モーターのブレーキモード

電気駆動におけるエンジンブレーキモードはエンジンと併用されます。電動ブレーキとして電動モータを使用することは、停止・後進時間の短縮、回転数の低減、走行速度の過度の上昇防止などを目的として広く実用化されている。

電気ブレーキとしての電気モーターの動作は、電気機械の可逆性の原理に基づいています。つまり、電気モーターは特定の条件下で発電機モードに切り替わります。

実際には、ブレーキには 3 つのモードが使用されます。

1) エネルギーをグリッドに戻す発電機 (回生)、

2) 電気力学的、

3) 反対。

直交座標系で機械特性を構築する場合、モータモードとブレーキモードにおけるモータトルクと回転速度の符号を決定することが重要です。このため、通常はモーター モードがメインとして使用され、このモードでのモーターの回転速度とトルクが正と見なされます。なお、モータモードの特性 n = f (M) は第 1 象限に位置します (図 1)。ブレーキモードにおける機械的特性の位置は、トルクと回転速度の符号によって異なります。

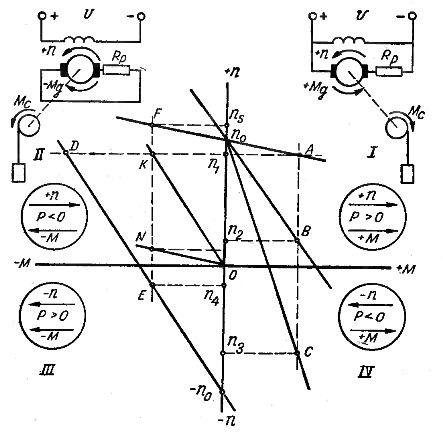
米。 1… モータモードとブレーキモードにおける並列励磁モータの接続図と機械的特性。

これらのモードと、並列励磁モーターの機械的特性の対応するセクションを考えてみましょう。

反対。

電気駆動装置の状態は、モータートルク Md と静的負荷トルク Mc の組み合わせによって決まります。例えば、ウインチで荷物をつり上げるときの定常回転数n1は、Md=Msのときの自然特性（図1のA点）でのエンジンの動作に相当します。モーターの電機子回路に追加の抵抗が導入されると、レオスタット特性 (速度 n2 および Md = Ms に対応する点 B) への移行により回転速度が低下します。

モーターの電機子回路の追加抵抗がさらに徐々に増加すると (たとえば、セクション n0 特性 C に対応する値まで)、まず負荷の持ち上げが停止し、次に回転方向が変化します。つまり、荷重は下がります（点C）。このような政権は野党と呼ばれます。

逆のモードでは、モーメント Md の符号は正になります。回転速度の符号が変化し、負になりました。したがって、反対モードの機械的特性は第 4 象限にあり、モード自体は生成的です。これは、トルクと回転速度の符号を決定するための受け入れられた条件から導き出されます。

実際、機械動力は積 n と M に比例し、モーター モードでは正の符号があり、モーターから作業機械に送られます。逆モードでは、n の負符号と M の正符号により、それらの積は負になるため、機械動力は逆方向、つまり作業機械からモーターへ伝達されます (発電機モード)。図では。 1 モーターおよびブレーキモードの文字 n および M は、丸と矢印で示されます。

反対モードに対応する機械特性のセクションは、第 1 象限から第 4 象限までのモーター モードの特性の自然な拡張です。

エンジンを反対のモードに切り替える考慮された例から、次のことがわかります。等c. モーターは、最後の回転速度に応じて、ゼロ値を越えると同時に符号を変え、主電源電圧に従って動作します: U = (-Д) +II amRfrom ここで、I am II am = (U +E) / R

電流を制限するために、通常は始動抵抗の 2 倍に等しい大きな抵抗がモーターの電機子回路に組み込まれます。逆モードの特徴は、シャフト側からの機械的動力とネットワークからの電気エネルギーがモーターに供給され、これらすべてが電機子の加熱に費やされることです: Pm+Re = EI + UI = Аз2(Ри + A次)

逆モードは、巻線を反対の回転方向に切り替えることによっても得られますが、一方、アーマチュアは運動エネルギーの蓄えにより同じ方向に回転し続けます (たとえば、静的無効モーメントを持つ機械 - ファンの場合)止まります）。

モーター モードに応じて符号 n と M を読み取るための許容条件に従って、モーターを逆回転に切り替えると、座標軸の正の方向が変化する必要があります。つまり、モーター モードは第 3 象限になります。そして反対派 - 2番目。

したがって、モーターがポイント A でモーター モードで動作していた場合、速度がまだ変化していない切り替えの瞬間、第 2 象限のポイント D で新しい特性になります。特性 DE (-n0) であり、速度 t = 0 でエンジンがオフにならない場合、点 E でこの特性が働き、速度 -n4 で機械 (ファン) が反対方向に回転します。

動電ブレーキモード

動電ブレーキは、モーターのアーマチュアをネットワークから切り離し、別の外部抵抗に接続することによって得られます (図 1、第 2 象限)。明らかに、このモードは独立励起 DC 発電機の動作とほとんど変わりません。自然な特性（直接n0）の作業は短絡モードに対応します。高電流のため、この場合のブレーキは低速でのみ可能です。

動電ブレーキモードでは、アーマチュアは U ネットワークから切断されるため、U = 0; ω0 = U / c = 0

機械的特性の方程式は次の形式になります。 ω = (-RM) / c2 または ω = (-Ri + Rext / 9.55se2) M

動電ブレーキの機械的特性は動力源によるもので、速度が低下するとエンジン ブレーキ トルクも減少します。

特性の傾きはモーターモードと同様に電機子回路の抵抗値によって決まります。電気力学的ブレーキは、ネットワークからモーターによって消費されるエネルギーが励起のみに費やされるため、その逆よりも経済的です。

電機子電流の大きさ、したがって制動トルクは、回転速度と電機子回路の抵抗によって決まります: I = -E/ R = -sω /R

エネルギーをグリッドに戻す発電機モード

このモードは、静的トルクの作用方向がモーターのトルクと一致する場合にのみ可能です。エンジンのトルクと作業機械のトルクという 2 つのモーメントの影響下で、ドライブの回転速度と e.等c. モーターが増加し始め、その結果、モーター電流とトルクが減少します: I = (U — E)/R= (U — сω)/R

速度がさらに増加すると、最初は U = E、I = 0、n = n0 のときに理想的なアイドル モードになり、次に e などのときになります。 c. モーターが印加電圧を超えると、モーターは発電機モードになり、ネットワークにエネルギーを供給し始めます。

このモードの機械的特性はモーター モード特性の自然な拡張であり、第 2 象限にあります。回転速度の方向は変化せず、以前と同様に正のままであり、モーメントは負の符号を持ちます。ネットワークにエネルギーが戻る発電機のモードの機械的特性の方程式では、モーメントの符号が変化するため、次の形式になります。 ω = ωo + (R / c2) M. または ω = ωo +(R/9.55°Cd3)M.

実際には、回生ブレーキモードは、高速で負荷を下げる場合など、静的モーメントが発生する可能性のあるドライブの高速でのみ使用されます。