電気モーターの加熱と冷却

さまざまな金属切断機、機構、機械の電気モーターの出力を正しく決定することは非常に重要です。電力が不足すると、機械の生産能力をフルに活用して、計画された技術プロセスを実行することができなくなります。電力が不十分な場合、電動モーターが早期に故障します。

電気モーターの出力を過大評価すると、系統的な過充電が発生し、その結果、モーターが不完全に使用され、低効率で力率が小さくなります (非同期モーターの場合)。また、エンジン出力が過大評価されると、資本コストと運用コストが増加します。

機械の動作に必要な電力、つまり電気モーターによって生成される電力は、機械の動作中に変化します。電気モーターの負荷は、モーターシャフトからの出力、トルク、またはオンタイム電流の依存性である負荷グラフ (図 1) によって特徴付けることができます。ワークの加工が終了したら、機械を停止し、ワークを測定し、ワークを交換します。その後、ロード スケジュールが再度繰り返されます (同じタイプの部品を処理する場合)。

このような変動負荷の下で正常な動作を保証するには、電気モーターは、この負荷スケジュールに従って、処理中に必要な最高の出力を生成し、連続動作中に過熱しないようにする必要があります。電気モーターの許容過負荷は、電気的特性によって決まります。

米。 1. 同じ種類の部品を加工する場合のスケジュールをロードする

エンジンがかかっているときは、 エネルギー（および電力）の損失発熱の原因となります。電気モーターによって消費されるエネルギーの一部は、その巻線の加熱やモーターの磁気回路の加熱に費やされます。 ヒステリシス そして摩擦と空気摩擦を運ぶ渦流。電流の二乗に比例する巻線の熱損失は、変数 (ΔРtrans) と呼ばれます。モーターの残りの損失は、負荷に多少依存し、通常、定数 (ΔРpos) と呼ばれます。

電気モーターの許容加熱は、その構造の最も耐熱性の低い材料によって決まります。この材料はコイルの絶縁体です。

電気機械の絶縁には次のものが使用されます。

• 絶縁化合物が含浸されていない綿および絹の布地、糸、紙および繊維状有機材料 (耐熱クラス U)。

• 同じ材料、含浸済み（クラス A）。

・合成有機フィルム（クラスＥ）。

• 有機結合剤を含むアスベスト、マイカ、ガラス繊維からなる材料 (クラス B)。

• 同じですが、合成結合剤と含浸剤を使用します (クラス F)。

• 同じ材料を使用しますが、シリコン結合剤と含浸剤を使用します（クラス H）。

• 結合剤を含まない、または無機結合剤を含む雲母、セラミック、ガラス、石英 (クラス C)。

絶縁クラス U、A、E、B、F、H では、それぞれ 90、105、120、130、155、180 °C の最高温度が許容されます。クラス C の限界温度は 180 °C を超え、絶縁クラスの特性によって制限されます。使用される材料。

電気モーターに同じ負荷がかかっている場合、周囲温度が異なるとその加熱は不均一になります。環境の設計温度 t0 は 40 °C です。この温度で、電気モーターの公称電力値が決定されます。電気モーターの温度が周囲温度を超えて上昇することを過熱といいます。

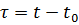
合成断熱材の使用は拡大しています。特に、シリコンシリコン絶縁体は、熱帯条件で動作する電気機械の高い信頼性を保証します。

エンジンのさまざまな部分で発生する熱は、断熱材の加熱にさまざまな程度で影響します。さらに、電動モーターの各部品間では熱交換が行われ、その性質は負荷条件に応じて変化します。

電気モーターの個々の部品の加熱と部品間の熱伝達が異なるため、プロセスの分析研究が複雑になります。したがって、簡単にするために、電気モーターは熱的に均一で無限の熱伝導体であると条件付きで仮定されます。一般に、電気モーターによって環境に放出される熱は過熱度に比例すると考えられています。この場合、モーターの絶対加熱温度が低いため、熱放射は無視されます。与えられた仮定の下で電気モーターの加熱プロセスを考えてみましょう。

電気モーターで動作すると、時間 dt の間に熱 dq が放出されます。この熱 dq1 の一部は電気モーターの質量によって吸収され、その結果、モーターの温度 t と過熱 τ が上昇します。残留熱 dq2 はエンジンから環境に放出されます。したがって、等式は次のように書くことができます

エンジン温度が上昇すると、熱量 dq2 が増加します。一定の過熱度では、電気モーター内で放出される熱と同じ量の熱が環境に与えられます。その後、dq = dq2 および dq1 = 0 となります。電気モーターの温度は上昇を停止し、過熱は定常値 τу に達します。

上記の仮定の下で、方程式は次のように書くことができます。

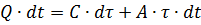
ここで、Q は電気モーターの損失による熱出力、J / s です。 A — エンジンからの熱伝達、つまりエンジンと環境との温度差が 1oC、J / s-deg の場合に、単位時間当たりにエンジンから環境に放出される熱量。 C はモーターの熱容量です。つまり、エンジンの温度を1℃上昇させるのに必要な熱量、J / deg.

方程式内の変数を分離すると、次のようになります。

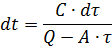
ゼロから時間 t のある現在値までの範囲の等式の左側と、電気モーターの初期過熱 τ0 から過熱の現在値 τ までの範囲の右側を積分します。

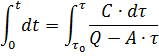
τ の方程式を解くと、電気モーターを加熱する方程式が得られます。

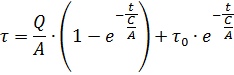
C / A = T と表し、この比率の次元を決定しましょう。

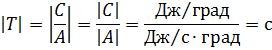
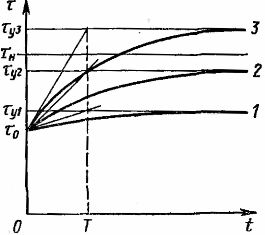
米。 2. 電気モーターの加熱を特徴付ける曲線

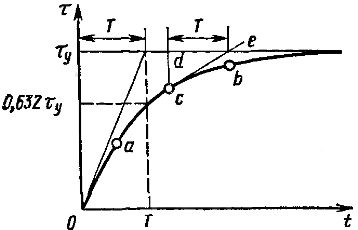
米。 3. 加熱時定数の決定

これは量 T と呼ばれ、電気モーターの加熱時定数の次元を持ちます。この表記に従って、加熱方程式は次のように書き直すことができます。

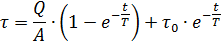
方程式からわかるように、定常状態の過熱値が得られます。

電気モーターの負荷が変化すると、損失の量が変化するため、Q の値も変化します。これにより、τу の値が変化します。

図では。図２は、異なる負荷値に対する最後の方程式に対応する加熱曲線１、２、３を示す。 τу が許容過熱度 τn の値を超えると、電動機の連続運転は許容できなくなります。式とグラフ (図 2) からわかるように、過熱度の増加は漸近的です。

値 t = 3T を方程式に代入すると、τy よりも約 5% だけ小さい τ の値が得られます。したがって、時間 t = 3T の間、加熱プロセスは実質的に完了したと考えることができます。

加熱曲線 (図 3) の任意の点で加熱曲線に接線を引き、次に同じ点を通る垂直線を引くと、接線と垂直線の間で閉じた漸近線の線分 de がスケール上に表示されます。横軸の は T に等しい。方程式で Q = 0 を取ると、モーター冷却方程式が得られます。

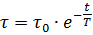
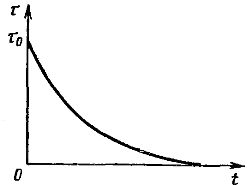
図に示す冷却曲線は、 4 はこの式に対応します。

加熱の時定数は、電気モーターのサイズと環境の影響に対する保護の形式によって決まります。オープンおよび保護された低出力電気モーターの場合、加熱時間は 20 ～ 30 分です。密閉型高出力電気モーターの場合、所要時間は 2 ～ 3 時間に達します。

上で述べたように、電気モーターの加熱について述べられている理論は近似的なものであり、大まかな仮定に基づいています。したがって、実験的に測定された加熱曲線は理論的なものとは大きく異なります。実験的な加熱曲線のさまざまな点について、図に示す構造が適用されるとします。図３より、時間の経過とともにＴの値が増加することがわかる。したがって、方程式に従って行われるすべての計算は近似値であると考えてください。これらの計算では、加熱曲線の開始点としてグラフで決定された定数 T を使用することをお勧めします。この T の値は最小であり、これを使用すると、エンジン出力に一定のマージンが得られます。

米。 4. エンジン冷却曲線

実験的に測定された冷却曲線は、加熱曲線よりもさらに理論的なものとは異なります。エンジン停止に対応する冷却時定数は、換気がない場合には熱伝達が減少するため、加熱時定数よりも大幅に長くなります。