AC 電源と電力損失

有効抵抗のみを持つ回路の電力は、有効電力 P と呼ばれます。これは、通常どおり、次の式のいずれかを使用して計算されます。

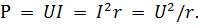
有効電力は、電流エネルギーの不可逆的（不可逆的）消費を特徴付けます。

鎖で縛られて 交流電流 回復不可能なエネルギー損失を引き起こす原因は、DC 回路よりも多くあります。これらの理由は次のとおりです。

1. 電流によるワイヤの加熱… 直流の場合、加熱はほぼ唯一のエネルギー損失です。また、直流と同じ値の交流の場合、表面効果により線材の抵抗が増加するため、線材を加熱するためのエネルギー損失が大きくなります。より高いです 電流周波数、影響が大きくなる 表面効果 そしてワイヤを加熱するための損失が大きくなります。

2. フーコー電流とも呼ばれる渦電流を生成するための損失… これらの電流は、交流によって生成された磁界内のすべての金属体に誘導されます。行動から 渦電流 金属体は発熱します。特に重大な渦電流損失はスチールコアで観察されることがあります。渦電流を生成するためのエネルギー損失は、周波数が増加するにつれて増加します。

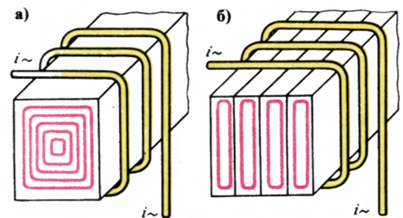
渦電流 — 巨大なコア内、b — 層状コア内

3. 磁気ヒステリシスの損失... 交流磁場の影響下で、強磁性コアが再磁化されます。この場合、コア粒子同士の摩擦が発生し、その結果コアが発熱する。周波数が増加すると、次のような損失が発生します。 磁気ヒステリシス 成長しています。

4. 固体または液体の誘電体における損失... このような誘電体では、交流電界により損失が発生します。 分子の分極つまり、電荷は分子の反対側に現れ、値は等しいが符号が異なります。分極した分子は場の作用を受けて回転し、相互摩擦を経験します。それにより、誘電体が発熱します。周波数が増加すると、損失が増加します。

5. 絶縁漏れ損失…使用されている絶縁物質は理想的な誘電体ではないため、絶縁漏れが観察されます。言い換えれば、絶縁抵抗は非常に高いですが、無限大にはなりません。この種の損失は直流でも存在します。高電圧では、電荷がワイヤの周囲の空気に流れる可能性さえあります。

6. 電磁波の輻射による損失…ACケーブル全般 電磁波を発する、周波数が増加すると、放射される波のエネルギーは急激に増加します（周波数の二乗に比例します）。電磁波は導体から不可逆的に放出されるため、電磁波の放射のためのエネルギー消費は、何らかのアクティブ抵抗の損失に相当します。無線送信アンテナでは、この種の損失は有用なエネルギー損失です。

7. 他の回路への電力伝送の損失...結果として 電磁誘導現象 AC 電力の一部は、ある回路から近くにある別の回路に転送されます。変圧器など、場合によっては、このエネルギー伝達が有益です。

AC 回路の有効抵抗は、リストされている回復不可能なエネルギー損失のすべてのタイプを考慮します。直列回路の場合、有効電力の比、つまりすべての損失の 2 乗に対する強さとして有効抵抗を定義できます。現在：

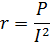
したがって、与えられた電流に対して、回路の有効抵抗が大きくなるほど、有効電力も大きくなり、つまり総エネルギー損失も大きくなります。

誘導抵抗のある回路部分の電力は無効電力 Q と呼ばれます。無効電力 Q は、無効エネルギー、つまり、回復不可能に消費されず、磁界内に一時的にのみ蓄積されるエネルギーを特徴づけます。有効電力と区別するために、無効電力はワットではなく、無効ボルトアンペア（var または var）で測定されます。この点で、以前は無水と呼ばれていました。

無効電力は、次のいずれかの式で求められます。

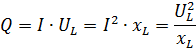
ここで、UL は誘導抵抗 xL の部分の電圧です。このセクションの電流は I です。

能動抵抗と誘導抵抗を備えた直列回路の場合、総電力 S の概念が導入されます。総電力 S は、総回路電圧 U と電流 I の積によって決定され、ボルト アンペア (VA または VA) で表されます。

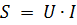
アクティブ抵抗のあるセクションの電力は、上記の式のいずれか、または次の式によって計算されます。

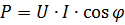
ここで、φ は電圧 U と電流 I の間の位相角です。

cosφの係数を力率…とよく言います。 «コサインファイ»… 力率は、総電力のうち有効電力がどのくらいかを示します。

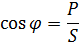
cosφ の値は、有効抵抗と無効抵抗の比率に応じて、0 から 1 まで変化します。回路内に 1 つしかない場合 反応性、その場合、φ = 90 °、cosφ = 0、P = 0となり、回路内の電力は純粋に無効になります。アクティブな抵抗のみがある場合は、φ = 0、cosφ = 1、および P = S、つまり、回路内のすべての電力が純粋にアクティブになります。

cosφが低いほど、皮相電力に占める有効電力の割​​合が小さくなり、無効電力が大きくなります。しかし、電流の仕事、つまりそのエネルギーが他の種類のエネルギーに移行することは、有効電力によってのみ特徴付けられます。無効電力は、発電機と回路の無効部分の間で変動するエネルギーを特徴づけます。

電力網にとって、それは役に立たないばかりか、有害ですらあります。無線工学では無効電力が必要であり、多くの場合に役立つことに注意してください。たとえば、無線工学で広く使用され、電気振動を生成するために使用される発振回路では、これらの振動の強度はほぼ純粋に反応性です。
ベクトル図は、cosφ を変更すると、電力が変化せずに受信機電流 I がどのように変化するかを示しています。

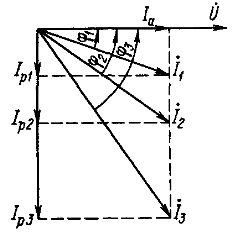
定電力およびさまざまな力率での受信機電流のベクトル図

ご覧のとおり、力率 cosφ は、交流 EMF 発電機によって生成される総電力の利用度を示す重要な指標です。cosφ <1 では発電機が積が有効電力より大きい電圧と電流。たとえば、電気ネットワークの有効電力が 1000 kW、cosφ = 0.8 の場合、皮相電力は次のようになります。

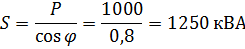
この場合、有効電力が電圧 100 kV、電流 10 A で得られるとします。ただし、皮相電力を得るには、発電機は 125 kV の電圧を生成する必要があります。

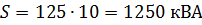
高電圧用の発電機の使用が不利であることは明らかであり、さらに、高電圧では、漏れの増加や損傷の発生を避けるためにワイヤの絶縁を改善する必要があります。これは電力網の価格の上昇につながります。

無効電力の存在により発電機の電圧を高める必要があるのは、有効抵抗と無効抵抗を備えた直列回路の特徴です。アクティブ分岐とリアクティブ分岐を備えた並列回路がある場合、発電機は単一のアクティブ抵抗で必要な電流よりも多くの電流を生成する必要があります。言い換えれば、発電機には追加の無効電流が負荷されます。

たとえば、上記の値 P = 1000 kW、cosφ = 0.8、S = 1250 kVA の場合、並列接続した場合、発電機は 100 kV の電圧で 10 A ではなく 12.5 A の電流を与える必要があります。 。この場合、発電機をより大きな電流に合わせて設計する必要があるだけでなく、この電流が流れる送電線の電線をより太くする必要があり、これにより線あたりのコストも増加します。発電機の線路および巻線に 10 A の電流用に設計されたワイヤがある場合、12.5 A の電流によりこれらのワイヤの発熱が増加することは明らかです。

したがって、余分ではありますが、 無効電流 無効エネルギーを発電機から無効負荷に、またはその逆に転送しますが、ワイヤのアクティブ抵抗により不必要なエネルギー損失が発生します。

既存の電気ネットワークでは、無効抵抗を持つセクションを、有効抵抗を持つセクションと直列または並列に接続できます。したがって、発電機は、有用な有効電力に加えて無効電力を生成するために、電圧と電流を増加させる必要があります。

これまでの話から、電動化がいかに重要であるかは明らかです。 cosφ値を大きくする…その減少は、電気ネットワークに無効負荷が含まれることによって引き起こされます。たとえば、アイドリング状態または完全に負荷がかかっていない電気モーターや変圧器は、比較的高い巻線インダクタンスを持っているため、重大な無効負荷が発生します。 cosφを高めるには、モーターとトランスが全負荷で動作することが重要です。それが存在します cosφを高めるいくつかの方法.

結論として、3 つの力はすべて次の関係によって相互に関連していることに注意してください。

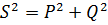
つまり、皮相電力は有効電力と無効電力の算術合計ではありません。電力 S は電力 P と Q の幾何学和であると言うのが通例です。

以下も参照してください。 電気工学におけるリアクタンス