電圧、抵抗、電力の三角形

ベクトル図のアイデアを持っている人なら誰でも、直角の電圧三角形がそれらの各辺で非常に明確に区別できることに簡単に気づくでしょう。各辺は、回路の合計電圧、アクティブ抵抗の電圧、および電圧を反映しています。 リアクタンスについて.

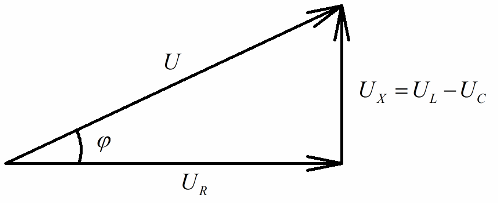
ピタゴラスの定理によれば、これらの電圧間の関係 (回路の合計電圧とそのセクションの電圧の間) は次のようになります。

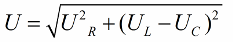
次のステップがこれらの電圧の値を電流で割ることである場合（電流は直列回路のすべてのセクションを均等に流れます）、次のようになります。 オームの法則 抵抗値が得られました。つまり、抵抗の直角三角形について話すことができます。

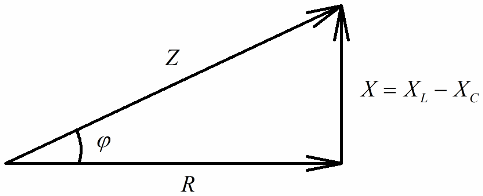
同様の方法 (電圧の場合など) では、ピタゴラスの定理を使用して、回路のインピーダンスとリアクタンスの間の関係を確立することができます。この関係は次の式で表されます。

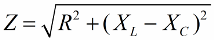
次に、抵抗値に電流を掛けます。実際には、直角三角形の各辺を特定の回数だけ増加させます。結果として、次の容量を持つ直角三角形が得られます。

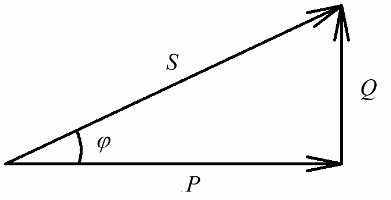
電気エネルギーの不可逆変換（設備内での作業の際、熱へ）に関連して回路のアクティブ抵抗で放出される有効電力は、エネルギーの可逆変換（生成）に関与する無効電力と明らかに関連しています。コイルとコンデンサの磁場と電場の影響を軽減し、電気設備に全電力が供給されます。

有効電力はワット (W) で測定され、無効電力は変動 (VAR - 無効ボルトアンペア) で測定され、合計は VA (ボルトアンペア) で測定されます。

ピタゴラスの定理によれば、私たちは次のように書く権利があります。

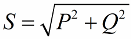
ここで、べき乗の三角形には角度 phi があり、その余弦は主に有効電力と皮相電力によって簡単に決定できるという事実に注目しましょう。 この角度の余弦 (cos phi) 力率と呼ばれます。これは、電気設備で有用な作業を行う際に総電力のうちどれだけが電力網に戻されないかを示します。

明らかに、力率 (最大値) が高いほど、プラントの運転に供給されるエネルギーの変換効率が高いことを示します。力率が 1 の場合、供給されたすべてのエネルギーが仕事を行うために使用されます。

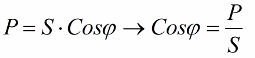
得られた比率により、力率、有効電力、ネットワーク電圧の観点から設備の消費電流を表すことができます。

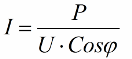
したがって、コサイン ファイが小さいほど、ネットワークが特定のジョブを実行するために必要な電流が増加します。実際には、この係数 (最大ネットワーク電流) によって伝送線路の伝送容量が制限されるため、力率が低いほど線路負荷が大きくなり、有効帯域幅が小さくなります (コサイン ファイが低いと制限が生じます)。コサイン ファイが減少する場合の電力線のジュール損失は、次の式からわかります。

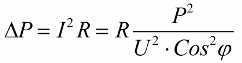
伝送線路のアクティブ抵抗 R では、負荷に対して反応性があるにもかかわらず、電流 I が大きくなるほど損失が増加します。したがって、力率が低いと単純に送電コストが上がると言えます。これは、コサインファイの増加が国家経済上の重要な課題であることを意味します。

総電力の無効分がゼロに近づくことが望ましく、そのためには電動機や変圧器を常に全負荷で使用し、使用終了時には停止させてアイドル状態にしないようにするとよいでしょう。無負荷では、モーターと変圧器の力率は非常に低くなります。ユーザーのコサイン ファイを増やす 1 つの方法は、次のとおりです。 コンデンサバンク と 同期補償器.