磁気回路の計算

電気機械や装置では、磁束 F が磁気回路 (強磁性コア) とこの磁気回路の空隙に集中します。この磁束の経路を磁気回路といいます。

磁気回路は電気回路と似ています。磁束 Ф は電流 I に似ており、誘導 В は電流密度に似ており、磁化力 (ns) Fн (H ∙ l = I ∙ ω) は e に相当します。等と

最も単純な場合、磁気回路はどこでも同じ断面を持ち、均質な磁性材料でできています。 nを決定するには。必要な誘導 B を提供するのに l ∙ ω が必要な場合、対応する強度 H が磁化曲線から決定され、磁力線の平均長さ l を掛けられます: H ∙ l = I ∙ ω = Fm。

ここから必要な電流Iやコイルの巻き数ωが決まります。

複雑な磁気回路は通常、異なるセクションと磁性材料を備えたセクションで構成されます。これらのセクションは通常直列に接続されているため、同じ磁束 F が各セクションを通過します。各セクションの誘導 B はセクションの断面に依存し、式 B = Φ∶S によってセクションごとに個別に計算されます。

誘導のさまざまな値について、強度 H は磁化曲線から決定され、回路の対応するセクションの電力線の平均長を掛けられます。個々の作品を合計すると、完全な n が得られます。 c. 磁気回路:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … これにより励磁電流またはコイルの巻数が決まります。

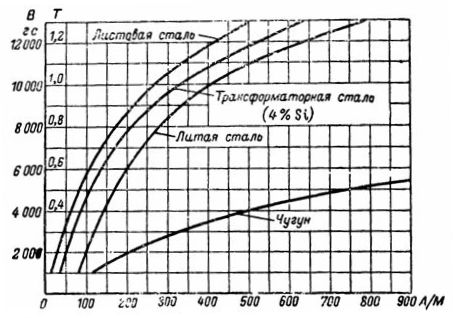
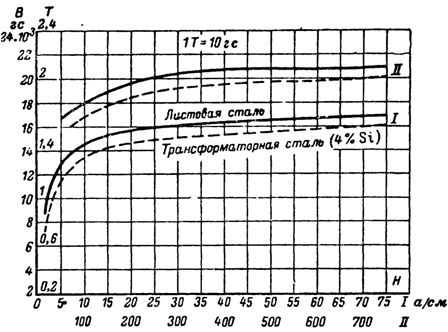
磁化曲線

の例

1. n となるためには、200 巻のコイルの励磁電流 I はいくらでなければなりません。 c. 鋳鉄リング内に磁束 Ф = 15700 Ms = 0.000157 Wb が生成されますか?鋳鉄リングの平均半径は r = 5 cm、断面の直径は d = 2 cm です (図 1)。

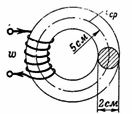
米。 1.

磁気回路の断面 S = (π ∙ d ^ 2) / 4 = 3.14 cm2。

炉心の誘導は B = Φ∶S = 15700∶3.14 = 5000 G です。

MKSA システムでは、誘導は B = 0.000157 Wb: 0.0000314 m2 = 0.5 T です。

鋳鉄の磁化曲線から、B = 5000 G = 0.5 T の場合、必要な強度 H は 750 A/m に等しいことが分かります。磁化の強さは、I ∙ ω = H ∙ l = 235.5 Av となります。

したがって、必要な電流 I = (H ∙ l) / ω = 235.5 / 200 = 1.17 A となります。

2. 閉磁路（図2）は変圧器の鋼板で構成されています。コア内に磁束 Ф = 160000 Ms = 0.0016 Wb を生成するには、0.5 A の電流でコイルを何回巻く必要がありますか?

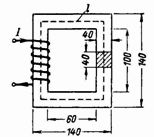
米。 2.

コア断面 S = 4 ∙ 4 = 16 cm2 = 0.0016 m2。

コア誘導 B = F / S = 160000/16 = 10000 Gs = 1 T。

変圧器鋼の磁化曲線によると、B = 10,000 Gs = 1 T の場合、強度 H = 3.25 A / cm = 325 A / m であることがわかります。

磁力線の平均長は l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0.48 m です。

磁化力 Fm = I ・ ω = H ・ l = 3.25 ・ 48 = 315 ・ 0.48 = 156 Av.

電流 0.5 A の場合、巻数は ω = 156 / 0.5 = 312 となります。

3. 図に示す磁気回路。図３の磁気回路は、δ＝５ｍｍの空隙を有することを除いて、前の例の磁気回路と同様である。どうあるべきなのか。磁束が前の例と同じになるように、つまり F = 160000 Ms = 0.0016 Wb になるようにコイル電流を調整しますか?

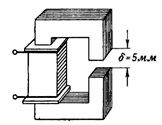
米。 3.

磁気回路には 2 つの直列接続されたセクションがあり、その断面積は前の例と同じ、つまり S = 16 cm2 です。インダクタンスも B = 10000 G = 1 T に等しくなります。

鋼磁線の平均長はわずかに短く、lс = 48-0.5 = 47.5 cm ≈ 0.48 mです。

磁気回路のこの部分の磁気電圧は Hc ∙ lc = 3.25 ∙ 48≈156 Av です。

エアギャップ内の磁界の強さは、Hδ = 0.8 ∙ B = 0.8 ∙ 10000 = 8000 A/cm です。

エアギャップ断面の磁気張力 Hδ ∙ δ = 8000 ∙ 0.5 = 4000 Av.

n を完了します。 c. は、個々のセクションの磁気電圧の合計に等しい: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13.3 A。

前の例で必要な磁束が 0.5 A の電流によって提供された場合、エアギャップが 0.5 cm の磁気回路の場合、同じ磁束を得るには 13 A の電流が必要です。このことから、磁気回路の長さに比べてわずかなエアギャップでも、必要な n が大幅に増加することがわかります。 v.およびコイル電流。

4. トランスの磁束は F = 72000 Ms と計算されます。 nの計算が必要です。s.および 800 ターンの一次巻線の励磁電流。トランスのコアには隙間δ=0.2mmがあります。変圧器コアの寸法を図に示します。 4. コアの断面積 S = 2 ∙ 3 = 6 cm2 (この形状のコアを備えた変圧器は装甲と呼ばれます)。

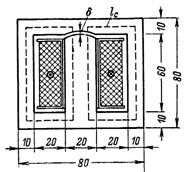
米。 4.

コアとエアギャップの誘導 B = F / S = 72000/6 = 12000 G。

B = 12000 G の変圧器鋼の磁化曲線に従って、強度: Hc = 5 A / cm を決定します。

鋼中の磁力線の平均長さは lс = 2 ∙ (6 + 3) = 18 cm です。

エアギャップ内の電圧 Hδ = 0.8 ∙ B = 9600 A / cm。

磁化力 I・ω = Hc・lc + Hδ・δ = 5・18 + 9600・0.02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0.35 A。

装甲コア内では、磁束は 2 つの部分に分かれ、サイド ロッドに沿って閉じられます。その断面は S / 2、磁力線の平均長さは lc です。結果として、磁気回路は、共通のコアＳおよび電力線長さｌｃを有する従来の変圧器の磁気回路と完全に類似する。

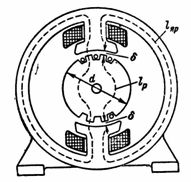
5. DC 機の磁束 F = 1280000 Mks。磁気回路には、平均磁力線長 l ＝ 80 cm の鋳鋼ヨーク、平均磁界長 l ＝ 18 cm の電気鋼板から組み立てられたローター、およびそれぞれ 0.2 cm の 2 つのエアギャップが含まれています。 = 8 ∙ 20 cm2;ローターとポールの断面 Sр = 12 ∙ 20 cm2... n を計算します。 p.とポールコイルの巻き数（最大励磁（励磁）電流が1Aの場合）（図5）。

米。 5.

ヨークとポールの誘導 Bя = Ф / Sя = 1280000/160 = 8000 G。

Bя = 8000 G での鋳鋼の磁化曲線によるヨークとポールの電圧は次のようになります。

H = 2.8 A/cm。

ヨークの断面の磁化力 HЯ ∙ la = 2.8 ∙ 80 = 224 Av.

ローター、ポール、エアギャップの誘導 Br = Ф / Ср = 1280000/240 = 5333 G。

鋼板製ローターの電圧 Br = 5333 Gs Hrp = 0.9 A/cm、

回転子セクションの磁気電圧 Hр ∙ lр = 0.9 ∙ 18 = 16.2 Av.

エアギャップ内の電圧 Hδ = 0.8 ∙ Bδ = 0.8 ∙ 5333 = 4266.4 A/cm。

エアギャップの断面における磁気電圧 Hδ ∙ 2 ∙ δ = 4266.4 ∙ 2 ∙ 0.2 = 1706.56 A。

n を完了します。 c. 別々のセクションの磁気電圧の合計に等しい: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ。 I ∙ ω = 224 + 16.2 + 1706.56 = 1946.76 平均

2極コイルの巻き数 ω = (I ∙ ω) / I = 1946.76 / 1≈2000。