絶縁体の絶縁耐力。計算例

誘電体 (絶縁) によって分離された導体 (たとえば、コンデンサ プレートや導電性ケーブル ワイヤ) 間の電圧 U が徐々に増加すると、誘電体内の電界の強度 (強度) が増加します。誘電体内の電界の強度も、ワイヤ間の距離が減少するにつれて増加します。

特定の電界強度では、誘電体で絶縁破壊が発生し、スパークまたはアークが形成され、回路に電流が発生します。絶縁破壊が起こる電界の強さを絶縁の耐電圧 Epr と呼びます。

絶縁耐力は絶縁体の厚さ mm あたりの電圧として定義され、V/mm (kV/mm) または kV/cm で測定されます。たとえば、滑らかなプレート間の空気の絶縁耐力は 32 kV / cm です。

導体が等しいギャップで分離されたプレートまたはストリップの形態である場合（たとえば、紙コンデンサ内）の誘電体内の電界の強度は、次の式で計算されます。

E = U / d、

ここで、U はワイヤ間の電圧 V (kV) です。 d — 誘電体層の厚さ、mm (cm)。

の例

1. プレート間の電圧が U = 100 kV の場合、プレート間の厚さ 3 cm の空隙内の電界強度はいくらですか (図 1)。

米。 1.

電界強度は次のとおりです: E = U / d = 100000/3 = 33333 V/cm。

このような電圧は空気の絶縁耐力（32kV/cm）を超えており、破壊する危険性があります。

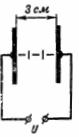
DC 損傷のリスクは、ギャップをたとえば 5 cm に増やすか、空気の代わりに電気段ボールなどの他のより強力な絶縁体を使用することによって防ぐことができます (図 2)。

米。 2.

電気段ボールの誘電率は ε = 2、絶縁耐力は 80,000 V/cm です。この場合、絶縁体の電界強度は 33333 V です。空気はこの力に耐えることができませんが、この場合の電気段ボールには 80,000/33333 = 2.4 の絶縁耐力の予備があります。これは、電気ボックスの絶縁耐力が 80,000/33333 = 2.4 であるためです。 80,000/32,000 = 空気の 2.5 倍。

2. コンデンサが電圧 U = 6 kV に接続されている場合、厚さ 3 mm のコンデンサの誘電体内の電界強度はいくらですか?

E = U / d = 6000 / 0.3 = 20000 V/cm。

3. 厚さ 2 mm の誘電体は 30 kV の電圧で破壊します。その電気の強さはどれくらいでしたか？

E = U / d = 30,000 / 0.2 = 150,000 V / cm = 150 kV / cm。ガラスにはこのような耐電圧性があります。

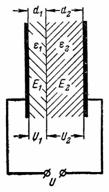
4. コンデンサのプレート間の空間は、同じ厚さの電気ボール紙の層と雲母の層で埋められます (図 3)。コンデンサのプレート間の電圧は U = 10000 V です。電気段ボールの誘電率は ε1 = 2、マイカの誘電率は ε2 = 8 です。電圧 U は絶縁層間にどのように分布し、各層の電界の強度はどの程度になるでしょうか?

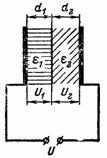
米。 3.

同じ厚さの誘電体層にわたる電圧 U1 と U2 は等しくありません。コンデンサの電圧は電圧 U1 と U2 に分割され、誘電率に反比例します。

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2。

U = U1 + U2 なので、2 つの未知数を持つ 2 つの方程式が存在します。

最初の式を 2 番目の式に代入します: U = 4 ∙ U2 + U2 = 5 ∙ U2。

したがって、10000 V = 5 ∙ U2; U2 = 2000 V; U1 = 4、U2 = 8000V。

誘電体層は同じ厚さですが、均等に帯電していません。誘電率が高い誘電体は負荷が少なく (U2 = 2000 V)、その逆も同様です (U1 = 8000 V)。

誘電体層内の電界強度 E は次のようになります。

E1 = U1 / d1 = 8000 / 0.2 = 40,000 V / cm;

E2 = U2 / d2 = 2000 / 0.2 = 10000 V/cm。

誘電率の違いにより、電界強度が増加します。ギャップ全体が 1 つの誘電体 (雲母や電気ボール紙など) だけで満たされている場合、電界強度はギャップ内にかなり均等に分布するため、より小さくなります。

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0.4 = 25000 V/cm。

したがって、誘電率が大きく異なる複雑な絶縁体の使用を避ける必要があります。同じ理由で、断熱材に気泡が形成されると故障のリスクが高まります。

5. 誘電体層の厚さが同じでない場合、前の例からコンデンサ誘電体の電界の強さを求めます。電気基板の厚さ d1 = 0.2 mm、マイカ d2 = 3.8 mm です (図 4)。

米。 4.

電界の強度は誘電率に反比例して分布します。

E1 / E2 = ε2 / ε1 = 8/2 = 4。

E1 = U1 / d1 = U1 / 0.2、E2 = U2 / d2 = U2 / 3.8 であるため、E1 / E2 = (U1 / 0.2) / (U2 / 3.8) = (U1 ∙ 3.8) / (0.2 ∙ U2) = 19 ∙ U1 / U2。

したがって、E1 / E2 = 4 = 19 ∙ U1 / U2、または U1 / U2 = 4/19 となります。

誘電体層の電圧 U1 と U2 の合計は電源電圧 U に等しくなります。U = U1 + U2。 10000 = U1 + U2。

U1 = 4/19 · U2 なので、10000 = 4/10 · U2 + U2 = 23/19 · U2 となります。 U2 = 190,000 /23 = 8260 V; U1 = U-U2 = 1740V。

雲母中の電場の強さは E2 ∙ 8260 / 3.8≈2174 V / cm です。

マイカの耐電圧強度は80,000V/mmであり、このような電圧にも耐えることができます。

電気段ボール内の電界強度は E1 = 1740 / 0.2 = 8700 V/mm です。

絶縁耐力は 8000 V / mm しかないため、電気段ボールはそのような電圧には耐えられません。

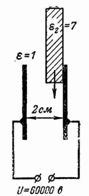
6. 2cm 離れた 2 枚の金属板に 60,000 V の電圧を接続し、空隙内の電界強度と、空隙内にガラスがある場合は金属板を挿入して空気およびガラス内の電界強度を測定します。厚さは1cmです（図5）。

米。 5.

プレート間に空気のみがある場合、その中の電界強度は次のようになります: E = U / d = 60,000 /2 = 30,000 V / cm。

電界の強さは空気の絶縁耐力に近いです。厚さ 1 cm のガラス板 (ガラスの誘電率 ε2 = 7) がギャップに挿入されると、E1 = U1 / d1 = U1 / 1 = U1 となります。 E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60,000-U2; 8 ∙ U2 = 60,000; U2 = 7500 V; E2 = U2 / d2 = 7500 V/cm。

ガラス内の電界の強さは E2 = 7.5 kV/cm、耐電圧は 150 kV/cm です。

この場合、ガラスには 20 倍の安全率があります。

エアギャップについては、次のようになります。 U1 = 60,000-7500 = 52500 V。 E1 = U1 / d1 = 52500 V/cm。

この場合、エアギャップ内の電界の強度は、ガラスのない最初の場合よりも大きくなります。ガラスを挿入すると、組み合わせ全体の強度は空気のみよりも低くなります。

ガラス板の厚さが導電板間のギャップと等しい場合、つまりガラス板の厚さが等しい場合にも破損の危険性が生じます。穴を開ける隙間には必然的に薄い空気の隙間ができるため、2cmです。

高電圧導体間のギャップの絶縁耐力は、誘電率が低く絶縁耐力が高い材料、たとえば、ε = 2 の電気ボール紙などで強化する必要があります。高誘電率の材料 (ガラス) の組み合わせは避けてください。 、磁器）と空気を油で置き換える必要があります。